Aus Schattenfächern einen Sonnenkalender machen (fakultativ)
| Publikation: | 3.4.2008 |
| Lernstufe: | 3 |
| Herkunft: | La main à la pâte, Paris. Originalversion: www.fondation-lamap.org/eratos |
Entdecken, wie man einen Schatten als "Kalender" benutzen kann
Mindestens zehn Tage (evtl. auch mehr) nach der letzten Messung der Schattenlängen, stellen die Schüler ihr Gnomon wieder in die Sonne, zusammen mit dem Blatt, auf dem der Verlauf des Schattens festgehalten wurde. Sie überprüfen, ob zu einer bestimmten Stunde der Schatten wieder an der gleichen Stelle wie beim letzten Mal ist. Aber nein! Schon bei der ersten Beobachtung am Morgen ist die Abweichung deutlich sichtbar, als hätte sich der Schatten verspätet (falls die Beobachtung nach dem 21. Dezember gemacht wird, davor ist es genau umgekehrt). Ganz schnell wird also über das alte ein neues Blatt Pauspapier gelegt. Wenn man dann den Schatten nachzeichnet, stellt man fest, dass der Schatten auch kürzer ist! (oder länger).
Wenn sofort ausgeschlossen wird, dass es an der Ausrichtung des Gnomons liegt, schließt man aus dieser Beobachtung, dass "die Sonne nicht mehr ganz an der gleichen Stelle ist wie beim letzten Mal!". Die Beobachtungen zu späteren Zeitpunkten an diesem Tag werden dieses Phänomen bestätigen, mit einer Ausnahme den Schatten am Sonnenmittag betreffend: Dieser Schatten ist genau an der gleichen Stelle, nur dass er etwas kürzer (oder länger) geworden ist. Wenn man jedoch zum Sonnenmittag eine ganz genaue Messung durchführt, wird man auch da eine kleine Abweichung feststellen können, die daher rührt, dass, verglichen mit unseren Uhren, der Zeitpunkt des Sonnenmittags nicht mehr ganz genau der gleiche ist wie vor 10 Tagen.
Andere Messungen werden zeigen, dass diese Abweichung, also die Abweichung zwischen Sonnenmittag und unseren Uhren, im Laufe des Jahres schwankt. Das liegt daran, dass unsere Uhren gewisse Unregelmäßigkeiten der Erdbewegung nicht berücksichtigen. Es handelt sich um Unregelmäßigkeiten, die daher rühren, dass die Achse, um die sich die Erde dreht, nicht senkrecht zur Ebene der Umlaufbahn unseres Planeten um die Sonne ist, und dass diese Umlaufbahn nicht kreis- sondern leicht ellipsenförmig ist.
Bemerkung: Man kann diese Fluktuationen auch anhand eines Kalenders nachvollziehen, in dem die Zeiten von Sonnenauf- und -untergang verzeichnet sind. Mit Hilfe einer Grafik können die Schwankungen der "Tagesmitte" im Verlauf eines Jahres untersucht werden (wobei der "Tagesmittag" der Zeitpunkt des Sonnenuntergangs minus der Zeitpunkt des Sonnenaufgangs, dividiert durch 2, ist).
Die Schüler werden bemerken, dass die Abweichungen der neuen Schatten im Vergleich zu den Schatten von vor 10 Tagen symmetrisch um den Sonnenmittag sind: Der Fächer hat sich ein wenig geöffnet (oder geschlossen).
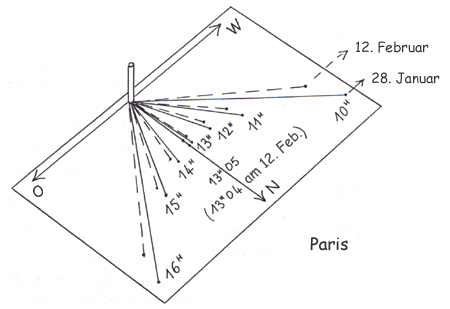
Abb. 11: Die Schatten des Gnomons an zwei verschiedenen Tagen
Den Grund für die Änderung der Schattenlängen können sie im Allgemeinen gut erklären, sie sind jedoch ziemlich ratlos, wenn es um eine Erklärung für das Öffnen (oder das Schließen) des Fächers geht. Dazu muss man die dreidimensionale Geometrie bemühen (Kegelschnitte): Das Ende des Schattens beschreibt im Laufe des Tages eine Kurve, die man Hyperbel nennt, die sich von einer Sonnenwende zur nächsten verändert und umkehrt; genau zwischen den beiden Sonnenwenden, zum Zeitpunkt der Tagundnachtgleichen, wird sie zu einer einfachen Geraden.
Daher ist es interessant, solche Schattenverläufe mehrmals im Jahr vorzunehmen, um diese Veränderung zu verfolgen.
Wichtige Bemerkungen hinsichtlich der "Sonnenkalender"
Abb. 12 zeigt – theoretisch – die Schattenfächer eines Gnomons (in unseren Breitengraden) an den Tagen der beiden Sonnenwenden und der beiden Tagundnachtgleichen. Man sieht, dass die Symmetrieachse dem Schatten des Sonnenmittags entspricht, den man zur Vereinfachung auf die nächste volle (der Tagesmitte am nächsten) Stunde auf- oder abgerundet hat. Daraus folgt, dass die beiden Hälften des Schattenverlaufs diesseits und jenseits des Sonnenmittags gleich breit sind.
In Wirklichkeit verhält es sich nicht so, wie die Schüler auch nicht versäumen werden zu bemerken: Die Breiten der beiden "Hälften" sind im Allgemeinen nicht exakt gleich, was zu einer mehr oder weniger stark betonten Unsymmetrie des Fächers führt. Warum ist das so? Das liegt daran, dass die Schatten jeweils zur vollen Stunde eingezeichnet wurden und der tatsächliche Zeitpunkt des Sonnenmittags an einem bestimmten Ort nicht unbedingt 12 Uhr (oder 13 Uhr) ist: Der Schatten um 12 Uhr (oder 13 Uhr) entspricht demnach nicht unbedingt der Symmetrieachse. Eine andere Bemerkung, diesmal bezüglich der Winkel, die durch die eingezeichneten Schatten eines Fächers gebildet werden: Sie sind in Wirklichkeit nicht gleich groß, am frühen Morgen und späten Nachmittag sind sie am kleinsten, um den Sonnenmittag am größten. Um das zu erklären, müsste man wieder auf die dreidimensionale Geometrie zurückgreifen. Das ist für die Schüler noch zu schwer und für die Fortsetzung des Projektes auch nicht erforderlich.

Abb. 12: Unterschiedliche Formen der Schattenverläufe zu Sommer- und Wintersonnenwende und an den Tagundnachtgleichen
Letzte Aktualisierung: 29.11.2023






