Der Einfluss der Schwerkraft auf die Erdbewegung

Autor:
Publikation:	1.9.2000
Herkunft:	La main à la pâte, Paris

Durch die Wirkung einer Gravitationskraft wird die geradlinige Bewegung eines Körpers verändert; sie ist dann weder geradlinig noch gleichförmig. Wenn wir uns auf zwei sich gegenseitig anziehende Körper beschränken, und keine weiteren Kräfte wirken, sind drei Fälle zu unterscheiden: Fall und Aufprall, Ablenkung, Eintritt in Umlaufbahnen. Untersuchen wir die drei Fälle unter der vereinfachenden Annahme, dass einer der Körper (A) sich nicht bewegt (dazu muss er von hinreichend großen Kräften festgehalten werden, was für keinen Körper im Weltraum der Fall ist, oder seine Masse muss so groß sein im Verhältnis zur Masse von Körper B, dass er sich vernachlässigbar wenig bewegt).

a) Aufprall oder Zusammenstoß

Wenn der Körper B eine praktisch verschwindende Anfangsgeschwindigkeit aufweist, oder sich genau auf A zu bewegt, wird A seine Bewegung beschleunigen; er wird sich immer schneller auf A zu bewegen bis zur Berührung der Oberflächen, also bis zum Aufprall mit all seinen Konsequenzen (im Weltall ist ein elastischer Stoß, wie zwischen zwei Billardkugeln, selten!). So etwas passiert jeden Tag mit zahlreichen Meteoriten, die vom Schwerefeld der Erde erfasst werden.

Wenn die Größe der Meteoriten zwischen der eines Staubkorns und einigen Millimetern liegt, entsteht beim Durchgang durch die Atmosphäre eine Sternschnuppe, Meteoriten von ein paar Zentimetern Größe bekommen einen Platz im Museum, und Meteoriten, die über 10 Meter groß sind, machen einen ansehnlichen Krater von mehreren Kilometern Durchmesser, wie man sie auf der Mondoberfläche sieht und auch an manchen Stellen der Erdrinde, wo die Erosion durch Wind und Regen sie nicht zum Verschwinden gebracht hat (Meteor Crater in Arizona – ca. 1,2 km, Manicouagan/Québec – ca. 70 km). Ein Meteorit von ein paar Kilometern (etwa 10!), schließlich, würde beim Aufprall eine so kolossale Energie freisetzen, dass auf der ganzen Erde Brände von unvorstellbaren Ausmaßen ausbrechen würden und für lange Zeit ein Großteil der entwickelten Lebensformen vom Globus verschwinden würde. Dies ist eine der Hypothesen, mit denen manche das abrupte Verschwinden der großen Dinosaurier zu erklären versuchen.

Internetseite mit Satellitenbildern von Meteoritenkratern und Asteorideinschlägen weltweit: www.lpi.usra.edu/lunar/analogs/impactcraters/

Animation zum Zusammenstoß zweier Körper
Die Animation als Bilderfolge

b) Ablenkung

Wenn sich Körper B nicht in Richtung A bewegt und seine Geschwindigkeit sehr groß ist im Verhältnis zu den Geschwindigkeitsänderungen aufgrund der Anziehung durch A, wird diese Anziehung nur zu einer Verbiegung der Bahn zu einem je nach den Anfangsbedingungen mehr oder weniger offenen Hyperbelast führen. B wird abgelenkt und findet fern von A wieder zu geradliniger und gleichförmiger Bewegung zurück.

Animation zur Ablenkung eines Körpers B durch einen Körper A.
Die Animation als Bilderfolge

c) Einlenken auf eine Umlaufbahn (Satellitenentstehung)

Wenn die Geschwindigkeit von B nicht groß genug ist, um den Körper aus der Anziehung durch A zu befreien (wie im Fall b), aber auch nicht so klein, dass er sich auf den Körper A zu bewegt und schließlich mit ihm zusammenstößt (wie im Fall a), wird B in eine Umlaufbahn um A eintreten, die immer eine Ellipse ist. Eine Ellipse ist eine geometrische Form, ein abgeflachter Kreis, zu dessen Konstruktion man zum Beispiel von zwei Zentren ausgehen kann, den so genannten Brennpunkten der Ellipse. Wenn B sich in einer Umlaufbahn um A bewegt, nimmt A einen der beiden Brennpunkte ein. Die Form der Ellipse (Länge der beiden Achsen und Exzentrizität) liegt ein für allemal fest, wenn man Ort und Geschwindigkeit (Richtung und Größe) von B in einem gegebenen Moment kennt, kann man die ganze Kurve berechnen.

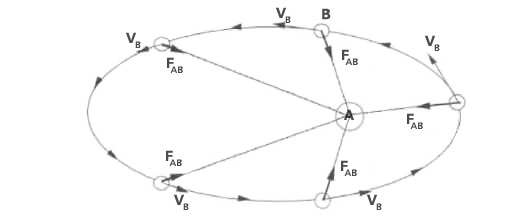
Einlenken auf eine Umlaufbahn

Wenn der Körper A nicht festgehalten ist, führen beide Körper eine Bewegung gleicher Art aus. Erde und Sonne beschreiben also eine Umlaufbahn um ihr Gravitationszentrum. Das liegt nur ein paar km vom Zentrum der Sonne entfernt (die Erdmasse wird auf 6×10²⁴ kg abgeschätzt, diejenige der Sonne auf 2×10³⁰ kg, die Sonne wiegt somit ungefähr 330 000 mal mehr als die Erde). Die Sonnenbahn, wenn es nur die Erde gäbe, wäre eine Ellipse mit einer großen Achse von ein paar km, was im Verhältnis zur Ausdehnung der Sonne zu vernachlässigen ist (Sonnenradius = 696 000 km, also 109 Mal mehr als der Erdradius). Im Übrigen macht die Gegenwart anderer, gewichtiger Planeten und tausender kleiner Körper im Sonnensystem die kleinen "Schwingungen" der Sonne viel komplizierter, sie bleiben jedoch vernachlässigbar gering.

Das Sonnensystem besteht also, so wie es definiert ist, aus der Menge der vom Gravitationsfeld der Sonne "eingefangenen" Körper, die sich in elliptischen Bahnen um sie herum bewegen. Manche von ihnen sind außerdem noch von Körpern, die größer sind als sie selbst, "eingefangen" und kreisen um diese. Dann spricht man von Satelliten. Das gilt für den Mond und – in Erweiterung der Bedeutung des Namens – für die "Monde" anderer Planeten.

d) Zusammenfassung

Die Erde kreist in elliptischer Umlaufbahn um die Sonne. Die Ellipse, die die Erde beschreibt, ist fast ein Kreis (die Exzentrizität ist beinahe null), denn ihr Perihel (der kleinste Abstand von der Sonne) liegt bei ungefähr 149 Millionen km, während der Aphel (größter Abstand der Erde von der Sonne) 153 Millionen km beträgt. Für die meisten Betrachtungen kann diese kleine Differenz vernachlässigt werden. Wir werden die Erdbahn daher als einen vollkommenen Kreis ansehen, der in 365 Tagen durchlaufen wird. Wenn wir die Erdbahn auf einem Blatt Papier darstellen, verschwindet diese Differenz in der Strichdicke.

Letzte Aktualisierung: 14.10.2024