Wie hat Eratosthenes den Winkel gemessen?
| Publikation: | 27.10.2007 |
| Lernstufe: | 3 |
| Dauer: | 15-20 Minuten für die schematische Darstellung und die Messung des Winkels; 45 Minuten bis 1 Stunde für die Auswertung der Messtabelle. |
| Material: |
Schematische Darstellung:
|
| Herkunft: | La main à la pâte, Paris. Originalversion: www.fondation-lamap.org/eratos |
Schematische Darstellung der Messungen des Eratosthenes
Teilen Sie die Schüler in Zweiergruppen auf und verteilen Sie das notwendige Material. Die Schüler sollen den Boden und den Obelisken mit seinem Schatten im vereinbarten Maßstab auf kariertes oder Millimeterpapier zeichnen. Im Maßstab 1:100 entspricht 1 cm auf der Zeichung 1 m in der Wirklichkeit und im Maßstab 1:50 entsprechen 2 cm auf der Zeichung 1 m in der Wirklichkeit. Die Kinder zeichnen danach die Hypotenuse des sich ergebenden Dreiecks (also die Strecke, die dem rechten Winkel gegenüber liegt), um den Sonnenstrahl und den zu messenden Winkel darzustellen.
Sie übertragen diesen Winkel auf Pauspapier (oder noch besser: auf transparentes Millimeterpapier) und schneiden ihn mit einem Rand aus (siehe Abb. 3). Dann legen sie ihn auf die vergrößerte Fotokopie eines Winkelmessers. Wenn sie sorgfältig und genau gearbeitet haben, sollten sie einen Winkel erhalten, der leicht größer ist als 7°, was dem von Eratosthenes gemessenen Wert von 7,2° gut entspricht. Weicht ihr Winkel jedoch stark davon ab, sollten sie nach den Ursachen für diese Diskrepanz suchen.
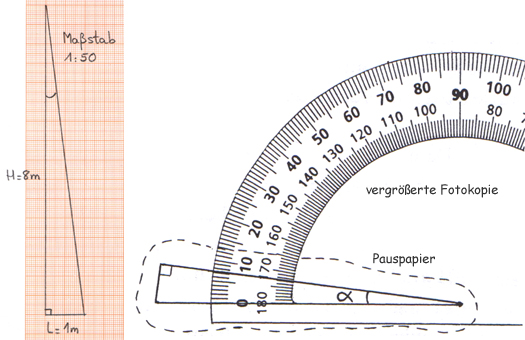
Abb. 3: Den durchgepausten Winkel mit Hilfe des fotokopierten Winkelmessers messen
Die Kinder werden feststellen, dass sie mit einer relativ großen Fotokopie des Winkelmessers den Winkel bis auf ein Viertelgrad genau messen können. Dies entspricht der Genauigkeit, mit der auch der griechische Gelehrte den Winkel gemessen hat. Sie werden dann auch verstehen, dass sich diese Genauigkeit mit einem "echten" Winkelmesser (der einfach zu klein ist) paradoxerweise nicht erzielen lässt, was sie später nachprüfen werden.
Sie kleben ihre Zeichnung in ihr Versuchsheft, daneben das auf den entsprechenden Teil der Fotokopie des Winkelmessers geklebte Stück Pauspapier, und schreiben einige Erläuterungen dazu.
Fakultativ: ein bißchen Übung!
Ihre Schüler können bei der folgenden Aufgabe spielerisch den Umgang mit dem Winkelmesser üben: "Wir haben die Messwerte wiedergefunden, die unser genialer Gelehrter in Alexandria das ganze Jahr über gemessen hatte, diese Messwerte der Schattenlänge des 8 m hohen Obelisken. Sie sind in der nachstehenden Tabelle angegeben – bis auf einige, die auf mysteriöse Weise verschwunden zu sein scheinen. Könnt ihr sie wiederfinden?"
Drucken Sie sich die folgende Tabelle mit Messwerten aus und löschen Sie mit Deckweiß einige der Messwerte für die Schattenlänge und den Winkel. Zu einem bestimmten Datum dürfen natürlich nicht beide Messwerte – die Schattenlänge und der Winkel – gleichzeitig gelöscht werden, da man ja den einen Wert braucht, um den anderen zu bestimmen. Die Tabelle wird anschließend fotokopiert und verteilt. Die Schüler sollen mündlich erläutern, wie bei der Suche nach den fehlenden Messwerten vorzugehen ist.
| Tag | 21. Jan. | 21. Feb. | 21. März | 21. Apr. | 21. Mai | 21. Juni | 21. Juli | 21. Aug. | 21. Sep. | 21. Okt. | 21. Nov. | 21. Dez. |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Länge des Schattens des Obelisken in Meter | 9,9 | 7,2 | 4,8 | 2,8 | 1,6 | 1,0 | 1,5 | 2,8 | 4,7 | 7,2 | 9,9 | 11,3 |
| Winkel zwischen den Strahlen und dem Obelisken in Grad | 51,1 | 41,8 | 31,0 | 19,3 | 11,1 | 7,2 | 10,8 | 19,2 | 30,6 | 42,0 | 51,2 | 54,7 |
Um die leeren Felder in der Tabelle zu füllen, werden die Schüler wieder zahlreiche schematische Darstellungen im verkleinerten Maßstab machen und mit dem Winkelmesser arbeiten müssen – eine gute Übung. Es ist auch eine gute Übung, um die Winkel aus den eigenen Messungen der Schattenlänge eines Gnomons – den bereits durchgeführten und den zukünftigen – zu bestimmen (siehe weiter unten).
Die Tabelle mit den Messwerten auswerten
Nachdem die Schüler die fehlenden Messwerte gefunden haben, wird ihnen auffallen, dass sich die Länge des Schattens (der jeweils am Sonnenmittag gemessen wurde) und die Neigung der Sonnenstrahlen im Laufe des Jahres verändern, und zwar in entgegengesetztem Sinn: Der Winkel erreicht am 21. Dezember seinen größten Wert und am 21. Juni seinen kleinsten, bei der Schattenlänge ist es umgekehrt. Diese Entwicklung haben sie wahrscheinlich schon bei den seit Beginn des Projekts gemachten Messungen der Schattenlänge bemerkt. Wenn nicht, wird diese Entdeckung ihnen bestimmt keine Ruhe lassen, und sie werden mehr darüber wissen wollen. Um herauszufinden, ob dies auch für ihren Wohnort gilt, müssen sie in den kommenden Wochen weitere Messungen der Schattenlänge durchführen und daraus den Winkel der Sonnenstrahlen ableiten, um deren Entwicklung bis zum Ende des Schuljahres zu verfolgen.
Inzwischen können sie die bereits durchgeführten Messungen auswerten, indem sie sie auf kariertes oder Millimeterpapier übertragen und mit dem Winkelmesser den Einfallswinkel der Sonnenstrahlen ermitteln. Diesen Wert können sie anschließend mit dem in Alexandria gemessenen Winkel vergleichen (dabei sollten sie das nächstmögliche Datum auswählen). Sie werden feststellen, dass sich die Werte unterscheiden und versuchen, eine Erklärung für diesen Unterschied zu finden. Um die Erklärung zu überprüfen, können sie die folgende Simulation machen.
Simulation mit einem Globus (oder einem Erd-Ball)
Rufen Sie Ihren Schülern die Simulation mit dem "Erd-Ball" in Erinnerung (siehe Teil 4 der Projektphase 3). Sie werden sich bestimmt noch erinnern, dass die Schatten der Gnomone immer länger wurden, je weiter man sich von Syene nach Norden oder nach Süden entfernte. Im ersten Fall zeigten die Schatten nach Norden, im zweiten nach Süden.
Letzte Aktualisierung: 29.11.2023






