8.5 (optional): Die Programmierkenntnisse vertiefen

Autoren:
Publikation:	30.9.2016
Lernstufe:	3
Übersicht:	Die Schüler vertiefen ihre Programmierkenntnisse. Sie wiederholen die Begriffe Variable, Test, Schleife, logischer Operator und definieren noch einmal genauer, was ein Algorithmus ist.
Angestrebte Kenntnisse:	Algorithmen: Mit einer Schleife im Programm kann man eine Anweisung wiederholen. Ein Test in einem Programm bestimmt, welche Aktion durchgeführt wer­den soll, wenn eine Bedingung erfüllt ist. Eine Bedingung ist ein logischer Ausdruck (eine logische Aussage), der (die) entweder wahr oder falsch sein kann. Mit logischen Verknüpfungen wie UND, ODER, NICHT kann man ele­mentare Ausdrücke (Aussagen) verknüpfen. Man erhält wieder einen logischen Ausdruck (eine logische Aussage). Manchmal muss man sich mit einem Algorithmus begnügen, der nicht die exakte Lösung liefert, sondern nur eine angenäherte Lösung. Maschinen: Eine Variable ist wie eine "Dose", die sich an einem bestimmten Spei­cher­ort im Computer befindet. Man kann in dieser Dose einen Wert abspeichern ("lagern"), um ihn später wieder zu benutzen oder zu ver­ändern. Für das Lösen mancher Aufgaben sind Maschinen (Computer) viel schnel­ler als Menschen.
Wortschatz:	Schleife, Variable, Test, Bedingung, logischer Ausdruck
Dauer:	ca. 4 Stunden
Material:	Für die Aktivität 1: ein Computerraum Für die Aktivität 2 (pro Gruppe mit 8 Schülern): 4 kleine Whiteboards mit Whiteboard-Stiften; ein Lappen ein Kartenspiel: Die Karten der Arbeitsblätter 34: "Kartenspiel – erster Teil" und 35: "Kartenspiel – zweiter Teil" säuberlich ausschneiden (und laminieren bzw. auf Pappe kleben) ein Spielwürfel Für die Aktivität 3: für jeden Schüler das Arbeitsblatt 36: "Aussagenlogik" für jede Vierergruppe das Arbeitsblatt 37: "Die Basisstation sichern" Für die Aktivität 4: für jeden Schüler das Arbeitsblatt 38: "Den kürzesten Weg finden" (optional) ein Brett (20 cm x 20 cm, 2 cm dick), in das in einem unre­gelmäßigen Muster etwa 20 Nägel geschlagen wurden (schön gerade!); eine Schnur (etwa 2 Meter lang; ein Ende wird an einen der Nägel gekno­tet); ein Filzstift
Herkunft:	La main à la pâte, Paris

Vorbemerkungen

Die folgenden Aufgaben erstrecken sich über mehrere Stunden und unterbre­chen die Programmierarbeit an dem Videospiel. Die Aufgaben dienen dazu, die bisherigen Programmierkenntnisse in anderen Kontexten wieder einzusetzen. Für die meisten Aufgaben wird kein Computer benötigt.

Die Aufgaben sind optional und völlig unabhängig voneinander. Man kann mit dem Programmieren des Videospiels fortfahren, ohne sie gemacht zu haben.

Um die Dynamik des Programmierens an dem Videospiel nicht zu zerstören, sollte man die hier beschriebenen Aufgaben möglichst parallel machen, viel­leicht im Mathematik- und/oder Deutschunterricht.

Die erste Aufgabe kann allerdings problemlos in eine Programmierstunde inte­griert werden. Man nimmt sich dafür einfach 10 Minuten Zeit, bevor die Schü­ler mit dem Programmieren des Videospiels weitermachen.

Aktivität 1: Schleifen – formative Evaluation

Am Computer, 10-20 Minuten

Diese formative Evaluation macht man am besten nach der Unterrichtsstunde 8.4 (Objekte sammeln und den Punktestand verwalten). Anhand einer Reihe von kleinen Übungen kann die Lehrerin bewerten, wie sich die Schüler den Be­griff der Schleife angeeignet haben. In der Unterrichtsstunde 8.4 haben die Schüler Endlosschleifen eingesetzt, hier lernen sie noch einen weiteren Schlei­fentyp kennen.

In der Unterrichtsstunde 4.3 (Mit Schleifen ein Programm vereinfachen) sollten die Schüler die Schreibweise eines Programms mit Hilfe einer Schleife vereinfa­chen. Hier machen wir es wieder genauso – diesmal mit Scratch anstatt mit Scratch Junior. Das Skript in Abb. 1 links lässt die Figur ein Quadrat ablaufen. Das Skript in Abb. 1 rechts bewirkt das Gleiche – die Schreibweise mit einer Schleife macht das Programm allerdings übersichtlicher. Wenn die Schüler schon gut im Programmieren sind, können sie das linke Programm selbstständig durch ein Programm mit Schleife ersetzen. Ansonsten gibt ihnen die Lehrerin alle Elemente – einzeln und ungeordnet. Die Schüler müssen die Befehle dann ordnen und miteinander verknüpfen, sodass auch dieses Programm die Figur ein Quadrat ablaufen lässt.

     

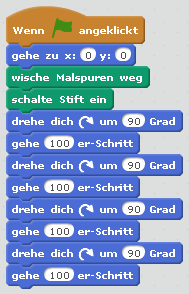
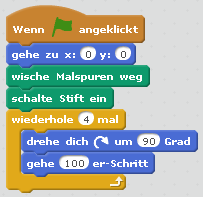
Abb. 1: Die Figur geht in die Mitte des Bühnenbilds und läuft im Quadrat, jeweils 100 Schritte (Pixel). Links: Skript ohne Schleife, rechts: Skript mit Schleife.

Wir empfehlen, diese Art von Übungen so oft zu wiederholen, bis die Schüler die Verwendung von Schleifen gut verstanden haben und sie ganz von selbst einsetzen, sobald sie mit sich wiederholenden Befehlen zu tun haben.

---

Aktivität 2: Ein Kartenspiel, mit dem der Begriff der Variablen vertieft wird

Ohne Computer, 1 Stunde

In dieser Aufgabe soll der Begriff der Variablen vertieft werden. Den Schülern steht dafür ein Kartenspiel zur Verfügung. Es ist interessant zu sehen, wie die Schüler mit jedem erneuten Spiel immer ausgefeiltere und kompliziertere Stra­te­gien entwickeln. Die Aufgabe kann im Mathematikunterricht bearbeitet wer­den (Kopfrechnen – es muss ständig der Punktestand neu berechnet wer­den) oder im Deutschunterricht (Was bedeuten die Texte auf den einzelnen Kar­ten?). Am besten ist es, wenn man mit kleinen Gruppen (8 oder 16 Schü­ler) arbeitet. Falls die Lehrerin mit der gesamten Klasse arbeiten will, sollte sie Zeit einplanen, um die Texte auf den Karten mit den Schülern durch­zugehen, bevor diese anfangen zu spielen. Sind die Schüler in Gruppen aufge­teilt, können sie sofort mit dem Spielen beginnen. Texte werden erst/nur dann besprochen, wenn die Schüler damit Schwierigkeiten haben.

Die Variablen, mit denen es die Schüler in dieser Aufgabe zu tun haben, sind die Punktestände der verschiedenen Spieler. Die Karten verändern diese Punk­testände. Zu Beginn werden nur die Karten verwendet, mit denen die Schüler einfache Rechenoperationen durchführen müssen. Anschließend kommen immer komplexere Karten hinzu, bei denen die Änderung des Punktestands an be­stimmte Bedingungen geknüpft ist.

Ausgangssituation, Erklärung des Spiels

In der Basisstation auf dem fernen Planeten sind die Abende lang. Sobald sie ihr Tagewerk erledigt haben, entspannen sich die Planetenforscher, indem sie Sport treiben oder Gesellschaftsspiele spielen. Ihr Lieblingsspiel wollen sie den Schülern beibringen. Das Spiel wird mit vier Mannschaften gespielt (am besten zwei Spieler pro Mannschaft, das heißt 8 Spieler pro Kartenspiel). Die Mann­schaften werden mit A, B, C und D bezeichnet.

Spielregeln

• Jede Mannschaft startet mit einem Punkt. Dieser Punktestand wird auf eine kleine Tafel (oder ein Blatt Papier) geschrieben.
• Jede Mannschaft bekommt vier Karten zugeteilt. Die restlichen Karten kommen verdeckt auf einen Stapel (Kartenstock).
• Die Schüler schauen sich ihre vier Karten an, ohne sie den anderen Mann­schaften zu zeigen.
• Der Reihe nach spielen die Mannschaften eine ihrer vier Karten aus. Sie lesen laut vor, was auf der Karte steht, und legen sie auf den Tisch. Die Anweisungen, die auf den einzelnen Karten stehen, ändern den Punkte­stand einer oder mehrerer Mannschaften. Die neuen Punktestände werden an der Tafel (auf dem Blatt Papier) aktualisiert.
• Wenn alle Karten ausgespielt wurden, hat die Mannschaft mit dem höchs­ten Punktestand gewonnen.

Die Lehrerin zeigt an der Tafel ein Beispiel. Sie skizziert einen Tisch und darum die vier Mannschaften A, B, C und D in Draufsicht. Neben jeder Mannschaft steht deren anfänglicher Punktestand, nämlich 1. Dann liest ein Schüler eine Karte vor, die die Mannschaft A ausgespielt hat. Die Schüler sollen sagen, wie sich durch diese Karte die Punktestände der einzelnen Mannschaften verän­dern. Die Lehrerin aktualisiert die Punktestände an der Tafel. Anschließend liest ein Schüler eine Karte vor, die von der Mannschaft B ausgespielt wurde usw. Das wird so lange fortgeführt, bis die Schüler verstanden haben, wie das Spiel geht.

Spielalternative: Man kann die vier Mannschaften auch kooperieren lassen. Alle Mannschaften halten ihre Karten wieder verdeckt, aber diesmal ist das Ziel, dass die Summe der vier Punktestände so hoch wie möglich ist.

Spiel mit den Karten 1 bis 24

Die Schüler spielen nur mit den Karten 1 bis 24 des Arbeitsblattes 34 (Karten­spiel – Teil 1). Diese Karten benennen explizit welcher Punktestand bzw. wel­che Punktestände geändert werden müssen, es werden keine Bedingungen ge­nannt.

Während der gemeinsamen Erörterung macht die Lehrerin die Schüler darauf aufmerksam, dass sich der Punktestand der einzelnen Mannschaften im Laufe des Spiels verändert hat. Sie führt das Adjektiv "variabel" ein. Variabel bedeu­tet, dass sich etwas verändert. Die Klasse diskutiert über die Rolle der kleinen Tafel. Auf dieser Tafel wird der Punktestand aktualisiert, man wischt den alten Punktestand weg und ersetzt ihn durch den neuen.

Wenn die Schüler bereits mit Scratch umgehen können, kann die Lehrerin:

• sie bitten, den vier Punkteständen Namen zu geben, zum Beispiel Punk­te­stand A, Punktestand B, Punktestand C und Punktestand D;
• ihnen zeigen wie man diesen vier Variablen am Anfang den Wert 1 zuord­net (Initialisierung der Variablen);
• den Begriff "Variable" einführen: Einer Variablen entspricht im Computer ein Speicher mit einer bestimmten Adresse, in dem der aktuelle Wert der Variablen "abgespeichert" wird.
• die Spielkarten in Scratch übersetzen lassen. Die Schüler beginnen mit den einfachsten Karten, d. h. mit den Karten 1 bis 8, und setzen die Über­setzungsarbeit mit den schwierigeren Karten fort. Die in Scratch übersetz­ten Karten ersetzen ab sofort die ursprünglichen Karten.

Spiel mit den Karten 1 bis 36

Die Schüler spielen das Spiel erneut, diesmal auch mit den Karten 25 bis 36 aus dem Arbeitsblatt 35 (Kartenspiel – Teil 2). Unter den neuen Karten gibt es solche, die den Punktestand einer anderen Mannschaft ändern (der Mann­schaft rechts, links oder gegenüber von der eigenen Mannschaft). Die Anzahl der Punkte hängt außerdem vom eigenen Punktestand bzw. vom Punktestand der anderen Mannschaften ab. Andere Karten wiederum enthalten eine Bedin­gung: "Wenn euer Punktestand ..., dann ...".

Nach und nach werden auch diese Karten in Scratch übersetzt. Jedes Mal, wenn eine Karte übersetzt wurde, wird die ursprüngliche Karte durch die ent­sprechende "Scratch"-Karte ersetzt.

Spiel mit den Karten 1 bis 48

Die Schüler spielen das Spiel erneut, diesmal auch mit den Karten 37 bis 48 aus dem Arbeitsblatt 35 (Kartenspiel – Teil 2). Unter den neuen gibt es zwei Karten, in denen Zufallszahlen vorkommen (es wird gewürfelt). Acht Karten sollen von den Schülern vervollständigt werden.

Die Schüler fahren mit der Übersetzungsarbeit fort. (Es müssen nicht unbe­dingt alle Karten übersetzt werden.)

Die Karten in Scratch übersetzen

Wie weiter oben bereits mehrfach erwähnt, sollen die Spielkarten nach und nach in Scratch übersetzt werden, beginnend mit den Karten 1 bis 8.

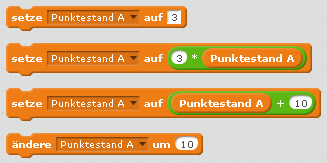
Abb. 1: Verschiedene Möglichkeiten, den Punktestand zu ändern. Der erste Befehl entspricht der Karte 1, der zweite der Karte 5, die nächsten beiden Befehle sind äquivalent und entsprechen der Karte 9.

Die verschiedenen Schülergruppen können sich die Übersetzungsarbeit auftei­len und das Ergebnis im Plenum besprechen. Manche Übersetzungen, insbe­sondere ab der Karte 25, sind nicht ganz einfach. Andere Karten kann man gar nicht in Scratch übersetzen – entweder ändern die Karten den Punktestand nicht oder der Punktestand hängt vom Kontext ab: von der Höhe des eigenen Punktestands, von den Punkteständen der anderen Mannschaften, von den Karten, die sich noch im Besitz der einzelnen Mannschaften befinden.

Für die Karte 32 zum Beispiel müsste man eine zweite Variable erzeugen, in der zwischenzeitlich ein Wert gespeichert werden könnte.

Zusammenfassung

Die Schüler fassen gemeinsam zusammen, was sie aus diesem Spiel gelernt haben.

• Im Laufe der Partien ändern sich die Punktestände der Mannschaften. Die Punktestände sind Variablen. Sie werden nach jeder Veränderung erneut gespeichert. Auch die Position der Mannschaften um den zentralen Tisch sowie die Anzahl der Karten, die sie noch auf der Hand haben, ändern sich. Das sind ebenfalls Variablen.
• In Programmiersprache würde man es so formulieren: In einer Variablen speichert man einen Wert, der sich während der Ausführung eines Pro­gramms, in dem die Variable vorkommt, ändert.

Mögliche Erweiterung

Die Schüler suchen nach Kontexten in ihrem Alltag, in denen ein Computer Va­ria­blen benutzt, um Daten zu speichern.

• Die auf einer digitalen Uhr angezeigte Zeit;
• die Geschwindigkeit eines Autos auf einem digitalen Tacho;
• Soll und Haben auf einem Bankkonto.

Sie recherchieren, wann sich die Werte dieser Variablen ändern bzw. wann sie verwendet werden. Zum Beispiel ändert sich die Anzeige der Uhr jede Sekun­de, und zu einer bestimmte Uhrzeit klingelt sie (wenn die Weckerfunktion ein­geschaltet ist). Genauso ändert sich der Stand eines Bankkontos jedes Mal, wenn man Geld ausgegeben hat oder jemand einem Geld überweist.

---

Aktivität 3: Ein Kartenspiel, mit dem der Begriff "logische Operatoren" vertieft wird

Ohne Computer, 1 Stunde

In der vorherigen Unterrichtsstunde (Objekte sammeln und den Punktestand verwalten) haben die Schüler Tests verwendet, zum Beispiel: "Wenn der Rover Eis oder Pflanzen einsammelt, dann erhöht sich der Punktestand". Die Lehrerin erklärt, dass der Teilsatz "Der Rover sammelt Eis/Pflanzen ein" eine elementare logische Aussage ist (man sagt auch: logischer Ausdruck) [1]. Eine logi­sche Aussage kann entweder wahr oder falsch sein. Leitet man eine logische Aussage mit der Konjunktion "Wenn" ein, erhält man eine Bedingung, die ent­weder erfüllt oder nicht erfüllt sein kann.

Die Aufgabe besteht aus zwei Teilen.

• Im ersten Teil machen sich die Schüler mit der Aussagenlogik vertraut. Dazu untersuchen sie die beiden Bilder im Arbeitsblatt 36 (Aussagenlogik).
• Im zweiten Teil müssen sie Bedingungen verknüpfen, damit der Alarm in der Basisstation ausgelöst wird. Dazu stehen ihnen im Arbeitsblatt 37 (Die Basisstation sichern) Karten mit Bedingungen sowie logischen Verknüpfun­gen zur Verfügung.

Übung: Aussagenlogik (jeder für sich)

Jeder Schüler bekommt das Arbeitsblatt 36 (Aussagenlogik) und schreibt ne­ben jede Aussage, ob diese – in der gegebenen Situation – wahr oder falsch ist, oder ob man keine Aussage über den Wahrheitsgehalt machen kann.

Die Antworten lauten:

• Aussage 1: WAHR (ziemlich eindeutig!).
• Aussage 2: FALSCH (auch eindeutig!).
• Aussage 3: WAHR (eine Tür ist immer entweder offen oder geschlossen).
• Aussage 4: FALSCH (eine Tür kann nicht gleichzeitig offen und geschlos­sen sein).
• Aussage 5: keine Aussage möglich (wir sehen die Tür gerade nicht und können daher nicht sagen, ob sie offen oder geschlossen ist).
• Aussage 6a: WAHR (beide Teilaussagen sind wahr).
• Aussage 6b: WAHR (es muss nur eine Teilaussage wahr sein; es sind so­gar beide Teilaussagen wahr).
• Aussage 7a: FALSCH (nur die erste Teilaussage ist wahr, es müssen aber beide wahr sein, damit die verknüpfte Aussage wahr ist).
• Aussage 7b: WAHR (nur eine Teilaussage muss wahr sein; das trifft für die erste zu).

Die Schülerantworten werden verglichen. Es wird so lange diskutiert, bis sich alle einig sind. Wahrscheinlich sind die Aussagen, die mit einem "ODER" ver­knüpft sind, für die Schüler schwieriger.

• Damit die Aussage "A oder B" WAHR ist, reicht es, wenn eine der beiden Aussagen A oder B WAHR ist. Es können auch beide WAHR sein.
• Damit die Aussage "A und B" WAHR ist, müssen beide Aussagen A und B WAHR sein.

Falls nötig, erfindet die Klasse weitere einfache Aussagen und überprüft, ob diese für das eine oder andere Bild des Arbeitsblattes 36 (oder in alltäglichen Situationen) wahr oder falsch sind. Wenn es für die Schüler einfacher ist, kann man die Aussagen bereits in einen Test verpacken. Beispiel: "Die Schulglocke läutet, wenn die Pause beginnt oder wenn der Unterricht beginnt oder wenn der Unterricht endet."

Anwendung logischer Ausdrücke – Die Basisstation wird gesichert

Die Lehrerin verteilt nun das Arbeitsblatt 37 (Die Basisstation sichern) an die in Vierergruppen aufgeteilten Schüler. Mit diesem Arbeitsblatt üben die Schüler den Umgang mit logischen Ausdrücken, und das im Kontext unserer kleinen Raumfahrt-Geschichte.

Die Aufgabe lautet: "Schneidet die Karten aus und kombiniert sie so, dass lo­gi­sche Ausdrücke entstehen. Ziel ist es, die Bedingung dafür zu beschreiben, dass der Alarm der Basisstation auslöst."

Zum Beispiel ertönt der Alarm, ...

• ... WENN "die Sicherheitsschleuse offen ist";
• ODER WENN "es dunkel wird" UND "der Rover nicht in der Basisstation ist";
• ODER WENN "der Sauerstoffpegel zu niedrig ist" UND "sich Menschen in der Basisstation befinden";
• ODER WENN "der elektrische Generator NICHT funktioniert";
• und so weiter und so fort.

Die Lehrerin überprüft, ob der Inhalt aller Karten gut verstanden wurde. Es gibt Karten mit Bedingungen (das sind die mit einem Bildchen) und es gibt logische Verknüpfungen (WENN, DANN, UND, ODER, NICHT). Die Verknüpfung "NICHT" ist neu und muss erklärt werden. Die Aussage, dass der Rover nicht in der Ba­sis­station ist, wird folgendermaßen geschrieben: "NICHT (Der Rover befindet sich in der Basisstation)". Bevor sich die Schüler selbst an das Lösen der Auf­gabe setzen, mag es hilfreich sein, sich gemeinsam ein paar einfache Beispiele zu überlegen – zunächst mündlich mit Sätzen, dann mit den Karten aus dem Arbeitsblatt. Sobald die Schüler das Prinzip verstanden haben, können sie selbst weitere Bedingungen finden und hinschreiben bzw. "hinlegen".

Abb. 3: Erste Bedingung zur Sicherung der Basisstation

Abb. 4: Zweite Bedingung zur Sicherung der Basisstation
(zum Vergrößern auf das Bild klicken)

Die Lehrerin lässt die Schüler jede Bedingung, die zum Auslösen des Alarms führt, präsentieren und diskutieren. Zum Schluss arbeitet die Klasse gemein­sam daran, alle Bedingungen in einem Ausdruck zu vereinen. Um die Übersicht zu behalten, sollte man nicht mit Klammern sparen. Man kann die Ausdrücke auch auf mehrere Zeilen verteilen (siehe Abb. 5).

Abb. 5: Alle Bedingungen zur Sicherung der Basisstation in einem Ausdruck
(zum Vergrößern auf das Bild klicken)

Zusammenfassung

Die Schüler fassen zusammen, was sie in dieser Unterrichtsstunde gelernt haben.

• Ein Test in einem Programm bestimmt, welche Aktion durchgeführt wer­den soll, wenn eine Bedingung erfüllt ist.
• Eine Bedingung kann entweder erfüllt (wahr) oder nicht erfüllt (falsch) sein (aber nicht beides gleichzeitig).
• Mit logischen Verknüpfungen wie UND, ODER, NICHT kann man elementare logische Aus­drücke verknüpfen.

Die Lehrerin schreibt die neuen Kenntnisse über Logik (logische Ausdrücke und logische Verknüpfungen) auf das Plakat "Was ist Informatik?".

---

Aktivität 4: Ein Algorithmus ist nicht immer perfekt – das Spiel mit dem Handelsreisenden

Ohne Computer, 1 Stunde

Ausgangssituation

In der vorherigen Unterrichtsstunde (Objekte sammeln und den Punktestand verwalten) haben die Schüler programmiert, dass der Rover so viel Eis und Pflanzen wie möglich einsammeln soll. Die Lehrerin erklärt nun, dass der Rover möglichst wenig Energie verbrauchen soll. Man hat also ein klassisches Opti­mie­rungsproblem zu lösen: Man kennt die Anzahl und den Ort der Eisbrocken und Pflanzen und muss nun einen Weg finden, der an allen Orten vorbeiführt und wieder an den Ausgangsort zurück­führt. Dieser Weg sollte der kurzmög­lichste Weg sein.

Die Lehrerin fragt die Schüler, ob es einen Algorithmus gibt, der das Problem lösen kann. Im Laufe der Diskussion werden aus dieser einen Frage zwei Fra­gen.

• Gibt es für dieses Problem eine Lösung? Gibt es einen Weg, der kürzer ist als alle anderen? Oder gibt es mehrere kürzeste Wege? Die Antwort lau­tet: "Wenn nicht alle Wege gleich lang sind, gibt es einen Weg, der kürzer ist als alle anderen (es kann auch mehrere kürzeste Wege ge­ben)."
• Gibt es eine Methode, mit der wir auf alle Fälle den kürzesten Weg herausbekommen? Die Schüler könnten zum Beispiel vorschlagen, dass man jeden möglichen Weg einzeichnet und dessen Länge misst.

Je nach Material, das der Klasse zur Verfügung steht, kann die Lehrerin be­schlie­ßen, dass die Aufgabe nur mit dem Arbeitsblatt 38 (Den kürzesten Weg finden) gelöst werden soll, oder erst mit dem Arbeitsblatt und dann mit einem Brett, Nägeln und Schnur.

Die Suche nach dem kürzesten Weg

Die Lehrerin verteilt das Arbeitsblatt 38 (Den kürzesten Weg finden). Ange­sichts der Anzahl der Wege, die sie einzeichnen und messen werden, ist es ratsam, ein Arbeitsblatt pro Schüler vorzusehen, auch wenn die Aufgabe in Gruppenarbeit gelöst wird. Es müssen alle Wege eingezeichnet werden, um zwei, drei oder vier Eisstücke einzusammeln. Der Weg beginnt an der Basis­station und endet dort auch wieder. Zwischendurch wird die Basisstation nicht angesteuert.

Gemeinsame Erörterung

Während der gemeinsamen Erörterung stellen die Schüler fest, dass die Anzahl der Wege sehr schnell sehr viel größer wird, wenn die Anzahl der Eisbrocken größer wird.

• Wenn es zwei Eisbrocken 1 und 2 gibt und die Basisstation mit B bezeich­net wird, gibt es zwei mögliche Wege: B12B oder B21B. Das ist eigentlich der gleiche Weg, der in zwei unterschiedlichen Richtungen durchlaufen wird.
• Bei drei Eisbrocken gibt es 6 Wege, davon drei unterschiedliche:
  - B123B und B321B (gleicher Weg, zwei Richtungen)
  - B132B und B231B (gleicher Weg, zwei Richtungen)
  - B213B und B312B (gleicher Weg, zwei Richtungen)
• Bei vier Eisbrocken sind es schon 24 Wege, davon 12 unterschiedliche:
  - B1234B und B4321B (gleicher Weg, zwei Richtungen)
  - B1243B und B3421B
  - B1324B und B4231B
  - B1342B und B2431B
  - B1423B und B3241B
  - B1432B und B2341B
  - B2134B und B4312B
  - B2143B und B3412B
  - B2314B und B4132B
  - B2413B und B3142B
  - B3124B und B4213B
  - B3214B und B4123B
  Auch wenn man alle Dubletten streicht, bleiben immer noch 12 mögliche Wege – zu viele, als dass die Schüler sie alle finden und in das gleiche Bild einzeichnen können.

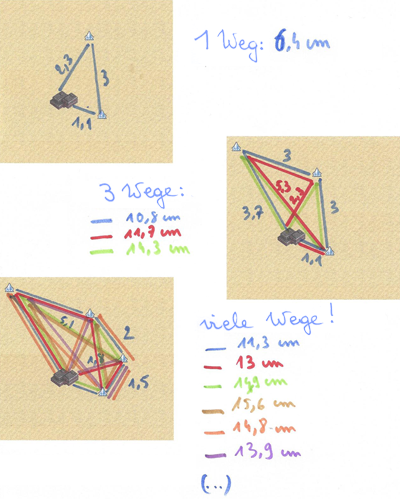
Abb. 6: Die Anzahl der möglichen Wege hängt von der Anzahl der Objekte ab, die eingesammelt werden sollen.

Die Suche nach dem kürzesten Weg – mit Brett, Nägeln und Schnur (optional)

Die Schüler hauen zunächst drei Nägel in ein Holzbrett (ein Nagel stellt die Ba­sis­station dar), später dann einen vierten und einen fünften. Sie knoten die Schnur an dem ersten Nagel fest und führen sie nacheinander um die anderen Nägel herum. Zum Schluss muss die Schnur wieder zum ersten Nagel geführt werden. Für jeden ausprobierten Weg wird mit einem Strich die Länge des We­ges auf der Schnur markiert. Auf diese Weise findet man letztendlich den kür­zesten Weg heraus. Diese Aufgabe ist identisch mit der vorherigen – mit einem physischen Gegenstand in der Hand (ein Brett mit Nägeln und einer Schnur) können die Schüler jedoch meist leichter einen "guten" (= kurzen) von einem "schlechten" (= langen) Weg unterscheiden.

Abb. 7: Veranschaulichung der Aufgabe des Handelsreisenden

Gemeinsame Erörterung

• Es gibt sehr viele mögliche Wege (bei drei Eisbrocken werden die Schüler sie in der Regel nicht alle überprüft haben).
• Am Anfang findet man schnell immer kürzere Wege, anschließend wird es mühsamer, die Wege werden höchstens noch ein paar Millimeter kürzer.
• Manche Schüler sind der Meinung, dass sie DEN kürzesten Weg gefunden haben. Ganz sicher kann man nicht sein, aber eins wird deutlich: Bei den kurzen Wegen gibt es keine Überkreuzungen und jeder Streckenabschnitt wird nur einmal durchlaufen.

Die Lehrerin erklärt, dass die Anzahl der möglichen Wege sehr schnell riesig wird, wenn man die Anzahl der Eisbrocken erhöht. Für 10 Eisbrocken sind es bereits fast 2 Millionen Wege. Sie fragt die Schüler, ob es ein Gerät gibt, das den kürzesten Weg finden könnte. Die Schüler antworten womöglich: mit ei­nem GPS-Gerät. Wenn man die Eisbrocken durch Städte ersetzt, ist die Auf­gabe des GPS ähnlich wie diejenige, die der Handelsreisende zu lösen hat. Aber wie ist so eine Aufgabe lösbar, wenn man nicht nur 20 Städte hat, sondern 2000?

Die Klasse sieht ein, dass man in so einem Fall nicht alle Wege nachmessen kann. Nicht einmal ein Supercomputer könnte das. Der Rechner in einem GPS-Gerät macht es ähnlich wie die Schüler mit ihrem Nagelbrett. Er wählt per Zufall einen Weg aus und ändert ihn mehrfach, um auf einen kürzeren Weg zu kommen. Wenn die Weglänge sich nur noch wenig ändert, hört das Gerät auf zu suchen und schlägt als Lösung einen der kürzesten Wege vor, die es "aus­gemessen" hat. Um die Wahrscheinlichkeit zu erhöhen, wirklich den kürzesten Weg zu finden, kann es zu Anfang mehrere Zufallswege auswählen und diese unabhängig voneinander variieren, um kürzere Wege zu finden.

Das GPS-Gerät liefert also nicht (mit Sicherheit) den kürzesten Weg, aber einen "ganz guten" Weg. Aus diesem Grund ist es auch nicht weiter verwun­der­lich, wenn zwei verschiedene GPS-Geräte nicht den gleichen Weg vorschla­gen. Sie enthalten oft nicht exakt die gleichen Karten und verwenden nicht unbedingt den gleichen Algorithmus.

Zusammenfassung

Die Schüler fassen zusammen, was sie in dieser Unterrichtsstunde gelernt haben.

• Manchmal ist ein Problem so langwierig und schwer zu lösen, dass man sich mit einem Algorithmus begnügen muss, der nicht die exakte Lösung liefert, sondern nur eine angenäherte Lösung.
• Für das Lösen mancher Aufgaben sind Maschinen (Computer) viel schneller als Menschen.

Die Lehrerin vervollständigt das Plakat "Was ist Informatik?".

Mögliche Erweiterung

Man kann die Wege vergleichen, die verschiedene Routenplaner anbieten (Google Maps und andere; einfach nach "Routenplaner" suchen), oder ver­schiedene GPS-Geräte. Die Schüler werden feststellen, dass Routenplaner und/oder GPS-Geräte für die gesuchte Strecke nicht unbedingt alle den gleichen Weg anzeigen, aber alle einen "eher kurzen".

---

Fußnote

1: Wir verwenden für diese Aufgabe den Begriff "Aussage", für die nächste den Begriff "Ausdruck". Der Begriff "Ausdruck" ist allgemeiner. Eine "Aussage" ist immer ein Satz oder Teilsatz, während ein "Ausdruck" zum Beispiel auch ein mathematischer Ausdruck sein kann (ein wahrer mathematischer Ausdruck ist z. B.: "5 > 3"; ein falscher mathematischer Ausdruck: "10 − 3 = 5").

© Sonnentaler/La main à la pâte | Impressum | Disclaimer | Datenschutz | RSS | E-Mail

© Sonnentaler / La main à la pâte  http://www.sonnentaler.net/