Die Bahnen sind stets elliptisch

Autor:
Publikation:	1.9.2000
Herkunft:	La main à la pâte, Paris

Wir haben bereits gesehen, dass die Bahn eines Planeten eine Ellipse ist. Das konnte als erster Johannes Kepler (1571-1630) dank der großen Genauigkeit der Beobachtungen seines Lehrers Tycho Brahe (1546-1601) feststellen. Kepler formulierte das erste der nach ihm benannten Gesetze des Sonnensystems so:

"Die Planeten beschreiben Bahnen um die Sonne, die die Form von Ellipsen haben. Die Sonne steht nicht im Zentrum der Ellipse, sondern seitlich in einem Punkt, den man "Brennpunkt" nennt."

Der Definition nach ist eine Ellipse "der geometrische Ort aller Punkte, für die die Summe der Entfernungen von zwei festen Punkten (Brennpunkten) eine Konstante ist". Wir empfehlen zur Illustration mit Bleistift und Faden eine Ellipse nach der "Gärtnermethode" zu Papier zu bringen.

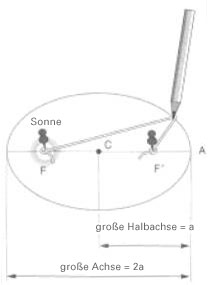
Eine Ellipse nach der Gärtnermethode zeichnen

Das geht ganz einfach so: Man drückt zwei Heftzwecken in den Punkten F und F' ins Papier. Damit sind die beiden Brennpunkte der Ellipse festgelegt. Jetzt verbindet man die beiden Punkte mit einem Faden, der länger ist als der Abstand FF'. Man hält den Faden mit einem Bleistift gespannt, den man über das Papier um die beiden Brennpunkte herumführt. Das Ergebnis ist eine Ellipse. Man stellt fest, dass die beiden Brennpunkte auf der großen Achse der Ellipse liegen (große Achse) und zwar in gleichem Abstand vom Mittelpunkt C, und dass die Länge der großen Achse (= 2a) gleich der Länge des Fadens ist.

Eine Ellipse kann mehr oder weniger abgeflacht sein, je nach Abstand der beiden Brennpunkte (der Kreis ist ein Spezialfall der Ellipse, die beiden Brennpunkte fallen dann zusammen). Man gibt das Maß der Abflachung durch einen Parameter an: Die Exzentrizität (die wir mit "e" bezeichnen) ist das Verhältnis von Abstand der beiden Brennpunkte und Länge der großen Achse: e = FF'/2a (für den Kreis gilt e = 0; je mehr sich die Exzentrizität einer Planetenbahn dem Wert 0 nähert, desto kreisförmiger ist die Bahn). Im Sonnensystem sind die Exzentrizitäten relativ gering. Pluto hat eine der exzentrischsten Bahnen (e = 0,249) im Sonnensystem, ebenso der Zwergplanet Eris (e = 0,44), während die Erdbahn mit e = 0,01675 beinahe kreisförmig ist.

Anhand von obiger schematischer Darstellung sieht man, dass der Abstand des Stiftes von der Heftzwecke, die die Sonne darstellt, nicht konstant ist. Wenn ein Planet die größte Sonnennähe erreicht, spricht man vom Perihel seiner Bahn, die größte Sonnenferne wird Aphel genannt. Im Fall der Erdbahn liegen die beiden Brennpunkte 4 Millionen km auseinander und der Abstand Erde-Sonne variiert zwischen ungefähr 147 Millionen km (Perihel) und 151 Millionen km (Aphel). Der Abstand der Planeten von der Sonne (hier dargestellt durch eine der Heftzwecken) variiert während des Umlaufs.

Achtung: Für die Jahreszeiten ist die Neigung der Rotationsachse der Erde gegen ihre Bahn und nicht etwa die (viel zu schwache) Änderung des Abstands Erde-Sonne verantwortlich.

Letzte Aktualisierung: 29.11.2023