3.4: Wie funktioniert eine Gangschaltung?
| Autoren: | |
| Publikation: | 9.3.2015 |
| Lernstufe: | 3 |
| Übersicht: | Die Schüler versuchen eine Gangschaltung zu verstehen; sie bauen ein Modell, das das Funktionsprinzip einer Gangschaltung veranschaulichen soll. |
| Angestrebte Kenntnisse: | Je kleiner die Ritzel am Hinterrad, desto schwerer wird es, in die Pedale zu treten. Dafür ist der Weg größer, den man mit einer Umdrehung der Tretkurbel zurücklegt. Eine Gangschaltung verfügt über einen Zahnkranz mit verschieden großen Ritzeln. |
| Wortschatz: | Gangschaltung, Gänge, Ritzel, Zahnkranz |
| Dauer: | 1 Stunde |
| Material: |
Für jede Gruppe:
|
| Herkunft: | La main à la pâte, Paris |
Ausgangsfrage
Die Lehrerin fragt: "Wir haben gesehen, wie das System Tretkurbel-Kette-Ritzel die Bewegung der Beine auf das Hinterrad überträgt. Gibt es Situationen, in denen das Treten besonders schwerfällt, die Anstrengung also sehr groß wird?". Die Schüler kommen schnell darauf, dass das Fahrradfahren bergauf anstrengend ist. Die Lehrerin fragt, was man machen kann, damit das Bergauffahren leichter wird, und lenkt die Diskussion auf die Gangschaltung.
Die Schüler suchen gemeinsam Möglichkeiten, wie sich die Gangschaltung im Modell nachbauen ließe. Falls nötig weist die Lehrerin auf den wesentlichen Unterschied zwischen großem und kleinem Ritzel hin: den Durchmesser. Man müsste also mit Zylindern mit verschiedenem Durchmesser das Funktionsprinzip einer Gangschaltung modellieren können. Die Lehrerin stellt das vorhandene Material vor.
Bau eines Modells zum Funktionsprinzip einer Gangschaltung (Gruppenarbeit)
Die Suche nach einem geeigneten Modell gestaltet sich ähnlich wie in der vorherigen Unterrichtsstunde, nur dass hier Zylinder mit unterschiedlichem Durchmesser verwendet werden. Wenn der "Tretkurbelzylinder" einen "Ritzelzylinder" mit einem kleineren Durchmesser antreibt, macht dieser mehr Umdrehungen als die Tretkurbel. Das Umgekehrte ist der Fall, wenn der "Tretkurbelzylinder" kleiner ist als der "Ritzelzylinder". Zur Feststellung der Anzahl der jeweiligen Umdrehungen werden die Zylinder mit Strichen versehen. Die Schüler stellen ihre Modelle schematisch dar.
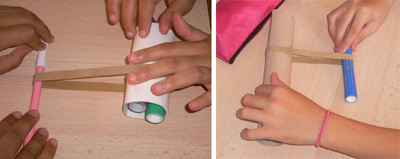
Abb. 1: Modelle zur Veranschaulichung des Funktionsprinzips einer Gangschaltung [1]
Die Experimente als Video: www.youtube.com/watch?v=Cp6dVjR_bGA
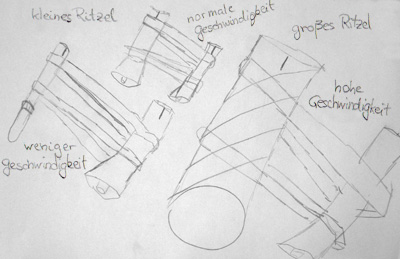
Abb. 2: Schülerzeichnungen zur Funktionsweise einer Gangschaltung [1]
Wenn entsprechende Baukästen vorhanden sind, verteilt die Lehrerin nun Material zur Herstellung eines Modells mit Kette und unterschiedlich großen Zahnrädern.
Abb. 3: Baukastenmodell [1]
Gemeinsame Erörterung
Um zu überprüfen, ob die Schüler die Mechanik der Kraftübertragung verstanden und sich das einschlägige Vokabular angeeignet haben, werden sie aufgefordert, die Bestandteile des Modells den Bauteilen des Fahrrads zuzuordnen. Welches Teil spielt welche Rolle? Die Diskussion dreht sich am Ende um die Rolle des Zahnkranzes am Hinterrad.
Die Schüler sollten unbedingt die Möglichkeit haben, an einem realen Fahrrad zu überprüfen, wie beim Gangwechsel der Durchmesser des jeweiligen Ritzels die Anzahl der Umdrehungen bestimmt, die das Hinterrad bei einer Umdrehung der Tretkurbel durchläuft. Je kleiner der Durchmesser, desto größer ist die Anzahl der Umdrehungen des Hinterrads – und damit die "zurückgelegte Strecke".
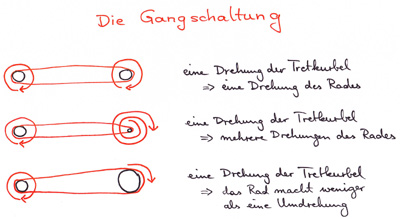
Abb. 4: Zur Funktionsweise einer Gangschaltung [1]
Pädagogische Anmerkung
Die Schüler haben Schwierigkeiten, den Zusammenhang zwischen Wegstrecke, Zeit und Geschwindigkeit herzustellen. Aus diesem Grund sollte man sich auf einen einzigen Parameter konzentrieren: zum Beispiel auf die zurückgelegte Strecke für eine Tretkurbelumdrehung. Der Kraftaufwand des Radfahrers hängt natürlich vom gewählten Ritzel ab, aber auch vom Rhythmus der Beinbewegung. Das Gleiche gilt für die Geschwindigkeit. Bei gleichem Rhythmus verlangt eine Umdrehung der Tretkurbel eine größere Anstrengung, je kleiner das Ritzel ist. Dafür fährt der Radfahrer mit größerer Geschwindigkeit (da er im gleichen Zeitraum eine größere Wegstrecke zurücklegt).
Zusammenfassung
Die Klasse formuliert gemeinsam eine Schlussfolgerung.
Beispiel: Bei gleichem Kettenblatt an der Tretkurbel ist der zurücklegte Weg umso größer, je kleiner das Ritzel am Hinterrad ist.
Multimediale Erweiterung
Abb. 5: Animation zur Funktionsweise einer Gangschaltung (auf Französisch)
In der Animation wird veranschaulicht, wie Tretrhythmus und Geschwindigkeit von der Wahl der Kettenblätter abhängen. Die (wenigen) Beschriftungen in der Animation sind auf Französisch. Durch Ausprobieren versteht man aber auch ohne Französischkenntnisse ziemlich schnell, was alles verändert werden kann. Die Geschwindigkeit der Kurbel lässt sich durch Drehen an den Pedalen (mit der Maus) verändern oder über den Geschwindigkeitsregler rechts. Im linken Kasten lässt sich die Anzahl der Zähne am vorderen und hinteren Kettenblatt ändern (avant = vorn, arrière = hinten, dents = Zähne, braquet = Übersetzung, plat = eben, descente = Abstieg, montée = Anstieg, cadence = Geschwindigkeit, tr/min = Umdrehungen/Minute).
Fußnote
1:
Abb. 1, 2 und 4: 5. Klasse von Cécile Perrin (Kremlin-Bicêtre)
Abb. 3: 5. Klasse von Kévin Faix (Kremlin-Bicêtre)
Letzte Aktualisierung: 14.10.2024
