Senkrechte und Waagerechte
| Publikation: | 26.10.2007 |
| Lernstufe: | 3 |
| Herkunft: | La main à la pâte, Paris. Originalversion: www.fondation-lamap.org/eratos |
In der Projektphase 2 werden die Begriffe senkrecht und waagerecht behandelt. In einem lokalen Maßstab sind diese Begriffe sehr intuitiv, aber was bedeutet senkrecht und waagrecht im Maßstab unseres Planeten? Dies wird im Folgenden erläutert.
Darstellung der Senkrechten und der Waagerechten
Die Senkrechte an einem bestimmten Punkt der Erde ist die von einem Senklot angezeigte Richtung. Eine an einer Schnur hängende Masse zieht die Schnur straff nach unten.
Jede Gerade, die in einer durch die Oberfläche einer ruhenden Flüssigkeit gekennzeichneten Ebene enthalten ist, stellt eine Waagerechte dar. Eine Ebene kann man z. B. mit Hilfe einer Wasserwaage bestimmen. Eine Wasserwaage ist ein möglichst langes Lineal, an dem ein Glasröhrchen (eine Libelle) angebracht ist, in dem Wasser und eine Luftblase eingeschlossen sind. Ist das Niveau waagerecht, befindet sich die Luftblase genau in der Mitte des Glasröhrchens. Ist dies nicht der Fall, wandert sie zu einem der Enden der Libelle.
An einem bestimmten Punkt gibt es eine Senkrechte und unendlich viele Waagerechte. Auf dem Schulhof sind alle Senkrechten einander parallel und senkrecht zu den Waagerechten. Auf der Erdoberfläche als Ganze gesehen sind die Senkrechten hingegen nicht alle parallel, sie treffen sich im Mittelpunkt der Erde. Auch die Waagerechten an verschiedenen Punkten der Erdoberfläche sind nicht parallel.
Um sich davon zu überzeugen, könnte man die unterschiedlichen Richtungen eines Senklots messen: Misst man den Winkel zwischen zwei 111 km (dies entspricht einem Breitengrad) voneinander entfernten Senkloten, würde man eine Differenz von 1° feststellen. Bei zwei 1 km voneinander entfernten Senkloten würde man eine Differenz von etwas weniger als 1/100°, d. h. 36 (Bogen-)Sekunden messen. Bei einem 10 m langen Klassenraum läge die Abweichung bei lediglich 0,36 (Bogen-)Sekunden, was mit einem Winkelmesser praktisch nicht mehr messbar ist. Bei zwei Punkten, die mehrere hundert Kilometer voneinander entfernt liegen, lässt sich der Winkel zwischen den Senkrechten messen.
Anmerkung: Winkelgrade werden normalerweise, wie bei der Zeit die Stunden, in (Bogen-)Minuten und (Bogen-)Sekunden unterteilt. Eine (Bogen-)Minute ist also genau 1/60 eines Grades, und eine (Bogen-)Sekunde ist 1/60 einer (Bogen-)Minute, also 1/3600 eines Grades. Jeder, der einmal mit einem Geodreieck gearbeitet hat, weiß, dass man damit Winkel im Gradbereich mit ausreichender Genauigkeit messen kann, bei Bruchteilen eines Grades (also im Bereich von Bogenminuten) wird es schon ziemlich schwierig, und die Bestimmung von Bogensekunden ist mit einem Geodreieck nicht mehr möglich. Dafür wären viel genauere Messinstrumente erforderlich.
Wir wissen, dass die Erde rund ist, aber an unserem Standort sieht sie eher flach aus. Wie lassen sich diese beiden Sichtweisen miteinander vereinbaren?
Unsere nähere Umgebung (die Straßen, die Mauer des Schulhofs) stellt einen so winzigen Teil der Erdkugel dar, dass man sie ohne größere Fehler zu machen als eben betrachten kann.
Im Maßstab unseres Planeten betrachtet, ist die Senkrechte an unserem Standort nichts anderes als die Verlängerung des Radius, der den Mittelpunkt der Erdkugel mit unserem Standort an der Erdoberfläche verbindet. Wenn man sich von einem Ort zu einem anderen begibt (z. B. von München nach Berlin), ändern diese Radien ihre Richtung und zeigen jeweils eine andere Senkrechte an. Beschränkt sich die Ortsveränderung auf eine kleine Entfernung (von einem Ende des Schulhofs zum anderen), sind die Winkel zwischen diesen Radien aber praktisch vernachlässigbar.
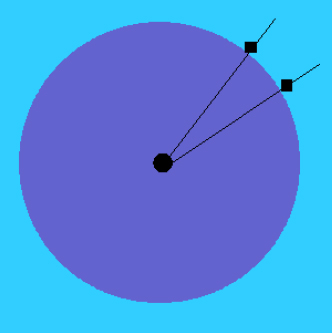
Abb. 5: Die Senkrechte auf der Erdoberfläche hat an jedem Punkt der Erde eine andere Richtung.
Im Maßstab des Planeten betrachtet ist die (örtliche) Waagerechte einfach in der Tangentialebene unseres Standortes auf der (kugelförmigen) Erdoberfläche enthalten. Über geringe Entfernungen fallen die Tangentialebenen praktisch zusammen, und zwei an den äußeren Enden eines Klassenraums angebrachte waagerechte Platten werden nicht gegeneinander geneigt erscheinen. Nicht dass der Winkel zwischen den beiden Platten exakt gleich Null wäre, aber er ist so winzig, dass man ihn nicht messen kann! Der Erdradius beträgt rund 6370 Kilometer, es bedarf also genügend großer horizontaler Entfernungen (mindestens einige Dutzend Kilometer), um die Erdkrümmung sehen zu können (z. B. ein klarer Horizont am Meer).
Die Senkrechte und die Waagerechte verstehen
Was haben Senkrechte und Waagerechte denn nun gemein, das zu einem physikalischen Verständnis der beiden Begriffe führen könnte? Es ist die Gravitation, die Kraft, die das Gewicht des Senklots anzieht und die Schnur strafft. Sie zieht auch das Wasser an und bewirkt, dass dessen Oberfläche waagerecht ist.
Was ist Gravitation genau?
Man kann sie als Eigenschaft der Materie betrachten: "Materie zieht Materie an." Zwei Körper ziehen einander umso stärker an, je größer ihre Masse und je geringer ihr Abstand voneinander ist. Lässt man z. B. ein Stück Kreide los, fällt es zu Boden. Warum? Weil die Erde und die Kreide einander anziehen.
In welche Richtung?
Jedes Teilchen der Erde zieht die Kreide an, aber wegen der Kugelgestalt der Erde (und auch wegen der annähernden Homogenität der Massenverteilung in den verschiedenen Schichten im Innern der Erde) kann man sagen, dass die Masse der Erde in ihrem Schwerpunkt konzentriert ist (den man in erster Näherung mit dem Mittelpunkt der Erde gleichsetzen kann). Die auf die Kreide wirkende Anziehungskraft der Erde ist also zum Mittelpunkt der Erde gerichtet: Die Kreide fällt zum Mittelpunkt der Erde. Ebenso richtet sich ein Senklot zum Erdmittelpunkt aus und stellt an einem bestimmten Ort die Senkrechte dar. Lässt man es fallen (ohne es zu werfen), folgt also auch das Kreidestück der Senkrechten!
Und wie steht es mit der Waagerechten?
Das gleiche Phänomen geschieht mit allen Teilchen einer bestimmten Wassermenge: Sie werden alle zum Mittelpunkt der Erde angezogen. Im Gleichgewicht (Ruhezustand) befinden sich alle Teilchen der Oberfläche einer Flüssigkeit (in einem Gefäß) im gleichen Abstand vom Erdmittelpunkt. Daher ist die Oberfläche der Flüssigkeit parallel zur Erdoberfläche: In einem örtlichen Maßstab ist die Oberfläche eben, im Maßstab unseres Planeten folgt sie dagegen der Erdkrümmung. Um uns herum ist das Meer (ohne Wellen) eben, aber über den gesamten Planeten betrachtet, eine Kugel.
Und noch einiges mehr ...
Geht die Senkrechte wirklich durch den Mittelpunkt der Erde? Die Antwort wäre ja, wenn die Erde völlig kugelförmig und die Verteilung ihrer Masse, auf den Mittelpunkt der Kugel bezogen, ganz symmetrisch wäre. Es ist aber erwiesen, dass die Erde eher ein Ellipsoid als eine Kugel ist. Genauer gesagt, ist sie an den Polen leicht abgeplattet. Es ist ein wenig so, als zöge sich ein "Wulst" um den Äquator. Diese Abweichung von einer Kugelform hat eine leichte Ablenkung der auf das Senklot einwirkenden Anziehungskräfte zur Folge. Das Senklot wird geringfügig zum Äquator hin abgelenkt und zeigt damit nicht ganz genau zum Erdmittelpunkt, sondern zum Schwerpunkt unseres Planeten. Für alle praktischen Zwecke im Rahmen des Projektes kann dieser Effekt jedoch vernachlässigt werden.
Letzte Aktualisierung: 29.11.2023






