Pädagogische Einführung zu dem kollaborativen Projekt "Auf den Spuren des Eratosthenes"

Publikation:	9.9.2008
Lernstufe:	3
Herkunft:	La main à la pâte, Paris. Originalversion: www.fondation-lamap.org/eratos

Dieses Projekt wird seit September 2000 auf der französischen Internetplatt­form von La main à la pâte angeboten. Seitdem haben schon Tausende von Schülern in der ganzen Welt den Umfang der Erde gemessen, genauso wie es vor über 2200 Jahren ein gewisser Eratosthenes bereits getan hatte. Lassen Sie uns hier in wenigen Worten das Prinzip des Experiments zusammenfassen: Man stellt einen Stab senkrecht an einen von der Sonne beschienenen Ort auf und misst die Länge seines Schattens. Und zwar wird diese Messung genau dann durchgeführt, wenn die Sonne am höchsten steht. Anschließend be­stimmt man den Winkel, den die Sonnenstrahlen mit der Senkrechten bilden und tauscht den herausgefundenen Wert für den Winkel mit einer auf einem anderen Breitengrad liegenden Partnerschule aus. Danach kann man auf zeich­nerischem Wege und mit Hilfe des Dreisatzes den Erdumfang berechnen.

Ein interdisziplinäres Projekt

Bei diesem Projekt kommen die Kinder, häufig auf spielerische Weise, mit zahl­reichen Wissensgebieten in Berührung und können sich dadurch vielfältige Kenntnisse aneignen (wovon viele Teil der Rahmenlehrpläne sind).

• Geschichte und Erdkunde: Um Schülern Zeit und Wirkungsort des Era­tosthenes näherzubringen, geht es zunächst um das alte Ägypten. Am Ende des Projektes lernen sie, sich auf der Erde zu orientieren, um den Standort eines oder mehrerer Partnerschulen finden zu können.
• Astronomie: An der Schattenlänge eines einfachen Stabes lässt sich die Bahn der Sonne im Laufe des Tages verdeutlichen. Weiterhin kann man den Zeitpunkt ablesen, an dem die Sonne ihren höchsten Stand erreicht, und man kann beobachten, wie sich die Bahn der Sonne mit den Jahres­zeiten verändert.
• Physik: Licht und Schatten stehen im Mittelpunkt des Projektes. Es wer­den entsprechende Experimente im Freien gemacht und die Beobachtun­gen anschließend im Klassenraum nachgestellt.
• Technik: Die Schüler entwerfen, bauen, erproben und verbessern die für die Messungen notwendigen Geräte: Gnomone, Senklote, Wasserwaagen, Winkelmesser und Quadranten.
• Mathematik, insbesondere Geometrie: In dem Projekt geht es um pa­rallele Geraden, um Winkel, Dreiecke, Kreise, um gleiche Winkel, Längen­verhältnisse usw.
  Anmerkung: Die Tatsache, dass acht- bis elfjährige Schüler erst elemen­tare Mathematikkenntnisse besitzen, könnte als echtes Hindernis für die Durchführung eines solchen Vorhabens erscheinen. Sicher, wenn man be­denkt, dass die zu erlernenden Begriffe nur formal gestreift werden kön­nen. Aber es ist durchaus möglich, sich diese Begriffe im praktischen Um­gang mit Pauspapier, Schablonen, Papiermessstreifen, Winkelmessern und sogar mir Schnurstücken (zur Messung von Kreisbögen) anzueignen. Die Kinder brauchen ja keine Eigenschaften von geometrischen Figuren herzu­leiten, sie sollen lediglich die Besonderheiten, die sie an einer geometri­schen Figur beobachten, untersuchen, oder aus einer angedeuteten Skizze die weitere "Entwicklung" dieser Figur erkennen. Man kann also hier von einer Art "experimenteller Geometrie" sprechen. Wenn dieses Projekt mit Oberschülern durchgeführt wird, wird man natürlich von ihnen logi­sches Denken und Abstraktionsvermögen verlangen, so dass einige Etap­pen des Projektes auf klassischere Art durchgenommen werden können.
• Sprache in Wort und Schrift: Die Sprache spielt natürlich bei allen Akti­vitäten eine Rolle, insbesondere beim experimentellen Vorgehen nach der La main à la pâte eigenen Methode: Die Schüler stellen Vermutungen an, schlagen Experimente vor, beschreiben ihre Beobachtungen und ziehen daraus Schlüsse; mündlich oder/und schriftlich. Für das Schriftliche haben sie ein Versuchsheft, in dem sie laufend ihre Beobachtungen, Gedanken und Erfahrungen festhalten können.
• Informations- und Kommunikationstechnologie: Das Internet brau­chen die Kinder zu Recherchezwecken und um die Ergebnisse ihrer Mes­sungen und Berechnungen mit einer oder mehrerer Partnerschulen aus­zutauschen.
• Bildende Kunst: Bei diesem Projekt kann jeder seine kreativen Fähig­keiten zeigen: Zeichnungen zur Geschichte des Eratosthenes, Comics, Modelle zur Veranschaulichung der Experimente, kalligrafische Spiele mit Hieroglyphen und griechischen Buchstaben.

Kinder mit schulischen Schwierigkeiten haben bei diesen Aktivitäten – insbesondere beim Experimentieren – Gelegenheit, ihre Fantasie, ihr Improvisationstalent und ihre manuelle Geschicklichkeit unter Beweis zu stellen. Gleichzeitig können sie sich in Teamarbeit üben. Die Anerkennung und Bewunderung seitens ihrer Mitschüler stärkt ihr Selbstbewusstsein und ermutigt sie dazu, sich auch in den anderen Fächern zu verbessern.

Ein abwandelbares Projekt

Der Projektablauf, den wir Ihnen vorschlagen, ist der ideale Ablauf, den Sie je­doch jederzeit modifizieren und den Umständen anpassen können: dem Alter, dem Niveau und der Motivation Ihrer Schüler, der Klassengröße, der Zeit, die Sie für das Projekt aufwenden können oder wollen und, nicht zu vergessen, den Launen des Wetters. Auch die Antworten und Vorschläge Ihrer Schüler werden manchmal die Marschroute bestimmen, und das Projekt damit eine manchmal unerwartete Richtung nehmen.

Fühlen Sie sich also völlig frei, den vorgeschlagenen Ablauf zu verändern. Sie sollten jedoch eins im Auge behalten: Entscheiden Sie sich lieber für Qualität als für Quantität. In der Tat, wenn Sie einige gut ausgewählte Experimente mit Ihren Schülern durchführen, und zwar im Sinne von La main à la pâte, wird das ausreichen, um Ihre Schüler mit der Arbeitsweise echter Forscherinnen und Forscher vertraut zu machen. Wenn Sie stattdessen eine Vielzahl ober­flächlicher Aktivitäten planen, wird das eher nicht gelingen.

Sie können den Ablauf also abkürzen, doch sollte er mindestens folgende fünf Etappen umfassen:

1. Gemeinsam nachweisen, dass die Erdoberfläche gekrümmt ist und die Sonnenstrahlen parallel.
2. Die Veränderung der Schattenlänge eines Stabes beobachten und daraus die Bahn der Sonne ableiten.
3. Den Sonnenmittag erkunden (d. h. den Zeitpunkt, zu dem der Schatten des Stabs am kürzesten ist).
4. Einen Gnomon verwenden, zur Bestimmung des Winkels, den die Sonnen­strahlen mit der Senkrechten bilden.
5. Die Messwerte einer Partnerschule für die eigenen Berechnungen des Erdumfangs verwenden. Dafür müssen auch die Standorte der eigenen und der Partnerschule bestimmt werden.

Abschließend noch einige Worte zum benötigten Material: Wie Sie sehen wer­den, handelt es sich um ganz einfaches, gebräuchliches, nicht teures Material: Zeichenpapier, Pappe, Paus- und Millimeterpapier, Schrauben, kleine Sperrholz­platten, Schnur, Taschenlampen, Bälle, ein Globus. Zu Beginn jeder der fünf Projektphasen wird angegeben, was benötigt wird.

Die Beobachtungen des Eratosthenes

Im Jahr 205 vor Christus schlägt der griechische Gelehrte Eratosthenes, da­mals Leiter der berühmten Bibliothek von Alexandria, eine rein geometrische Methode zur Messung des Erdumfangs (genauer: des durch die Pole gehenden Meridians) vor. Dazu muss man am Tag der Sommersonnenwende zum Sonnen­mittag – wenn die Sonne in der Nordhalbkugel ihren höchsten Stand über dem Horizont erreicht – zwei Schatten beobachten, der eine in Alexandria und der andere in Syene (dem heutigen Assuan). Syene liegt ungefähr 800 km südlich von Alexandria (diese Entfernung wurde mit Hilfe der Zeit abgeschätzt, die Kamelkarawanen benötigten, um von der einen zur anderen Stadt zu gelan­gen). In Syene (das ungefähr auf dem Wendekreis des Krebses liegt) steht die Sonne an diesem Tag und zu diesem Zeitpunkt senkrecht, so dass ihre Strah­len auf den Grund der Brunnenschächte fallen und die Schatten vertikaler Gegenstände verschwinden. In Alexandria steht die Sonne dagegen nicht senkrecht und die gleichen Gegenstände besitzen einen – sehr kurzen – Schatten. Eratosthenes misst zu diesem Zeitpunkt die Schatten eines Obe­lisken, dessen Höhe ihm bekannt ist, und er leitet daraus den Winkel ab, den die Sonnenstrahlen mit der Senkrechten bilden: Er erhält einen Wert von 7,2° (siehe Abb. 1).

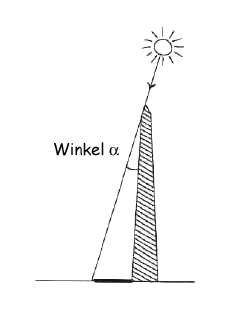
Abb. 1: Der Winkel zwischen den Sonnentrahlen und der Senkrechten

Diese Beobachtungen lassen ihn zwei Hypothesen aufstellen:

1. Die Erde ist flach (Abb. 2a). Dann müsste die Sonne allerdings nah genug sein, damit ihre Strahlen, wenn sie auf Gegenstände fallen, die einen gewissen Abstand voneinander haben, mit deutlich unterschiedlichen Winkeln einfallen. Wie man in Abb. 2a sehen kann, führen die divergenten Sonnentrahlen auf einer flachen Erde dazu, dass ein und derselbe Gegenstand an verschiedenen Orten der Erdoberfläche einen unterschiedlich langen Schatten hat, bzw. überhaupt keinen Schatten, wenn er direkt unter der Sonne steht (dann ist der Winkel zwischen Gegenstand und Sonnenstrahlen null).

2. Die Erde ist nicht flach (Abb. 2b), ihre Oberfläche ist gekrümmt und viel­leicht sogar kugelförmig. In diesem Fall würden die unterschiedlich langen Schatten auch bei parallelen Sonnenstrahlen zustande kommen. Dies setzt allerdings voraus, dass die Sonne weit genug, ja sehr, sehr weit entfernt ist – andernfalls könnten die Strahlen nicht überall auf der Erde parallel sein.

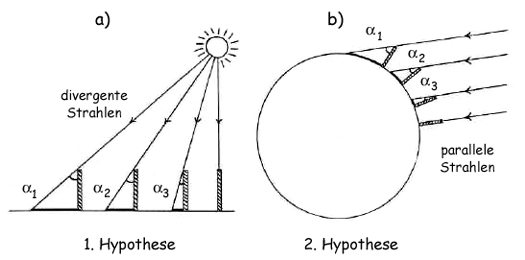
Abb. 2: Die 2 Hypothesen des Eratosthenes

Eratosthenes entscheidet sich für die zweite Hypothese. In der Antike wurde schon länger vermutet, dass die Erde nicht plan ist. Man stützte sich dabei auf diverse Beobachtungen, die eine gewisse Krümmung ihrer Oberfläche nahe­legen: Der Seemann an der Spitze seines großen Mastes erblickt als erster die ferne Küste; der Beobachter an der Steilküste sieht das zum Horizont segelnde Schiff länger als derjenige, der am Strand geblieben ist; der Polarstern hat in Griechenland nicht die gleiche Höhe über dem Horizont wie in Ägypten; und schließlich zeigt bei Mondfinsternissen der auf den Mond fallende Schatten der Erde einen kreisförmigen Ausschnitt. Von der Kugelform der Erde überzeugt, skizziert unser genialer Gelehrter seine verblüffend einfache und berühmt ge­wordene geometrische Zeichnung (Abb. 3), mit der er die Länge des Erd­umfangs (den durch Alexandria und Syene gehenden Meridian) auf einfachem Wege berechnen wird. Aber sehen Sie selbst!

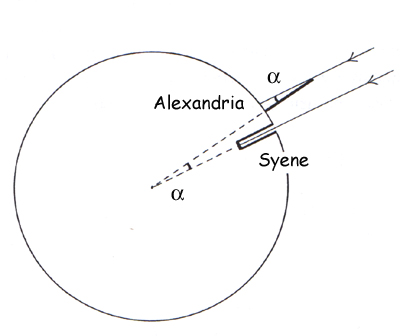
Abb. 3: Die Zeichnung des Eratosthenes

Wenn die Erde rund ist und man die Senkrechte in Alexandria (Obelisk) und in Syene (Brunnenschacht) verlängert, treffen diese beiden Senkrechten sich per definitionem im Erdmittelpunkt. Außerdem weiß Eratosthenes, dass Alexandria und die genau südlich davon gelegene Stadt Syene ungefähr auf dem gleichen Meridian liegen. Da die Sonnenstrahlen parallel sind, entspricht der von den beiden Senkrechten im Erdmittelpunkt gebildete Winkel dem Winkel, der mit Hilfe des Schattens des Obelisken gemessenen wurde (7,2°). Dieser Winkel steht zu den 360° des Kreises im gleichen Verhältnis wie die Entfernung zwi­schen den beiden Städten (etwa 800 km) zum Umfang der Erde. Sie erraten schon, wie es weiter geht: 360° geteilt durch 7,2° ergibt 50; und 800 km mal 50 macht 40 000 km (die Länge, die man später mit anderen Verfahren auch gefunden hat).

Und jetzt noch etwas für Mathematikfans

Wie weiter oben erwähnt, lassen sich die Beobachtungen des Eratosthenes auch unter der Annahme einer flachen Erde und einer sehr nahen Sonne ver­stehen. Mit den Angaben des Eratosthenes kann man sogar genau berechnen, wie weit die Sonne dann von der Erde entfernt sein müsste. Bei einer flachen Erdoberfläche wäre der Tangens des Winkels von 7,2° gleich der Entfernung Syene–Alexandria (800 km) dividiert durch die Entfernung Erde–Sonne: Daraus ergibt sich, dass die Sonne 800 km / tan 7,2 = ca. 6500 km (das entspricht dem Erdradius) von der Erde entfernt wäre. Das wäre außerordentlich nah. Heute weiß man, dass die Sonne ungefähr 150 Millionen Kilometer von uns entfernt ist.

Ein Versuchsprojekt auf die Klasse zuschneiden

Sie werden dieses Experiment in Kooperation mit einer anderen Klasse (deren geografische Koordinaten wir Ihnen angeben werden) durchführen, allerdings ohne Obelisk und ohne Brunnenschacht! Ein einfacher, senkrecht stehender Stab wird genügen, sowohl für Ihre Klasse als auch für Ihre Partnerklasse. Die beiden Stäbe sollten möglichst gleich lang sein, um den Vergleich der Schat­tenlängen zu erleichtern. Es muss auch nicht unbedingt eine der beiden Schu­len auf dem Wendekreis des Krebses liegen! Dagegen ist es von Vorteil, wenn beide Schulen auf ganz unterschiedlichen Breitenkreisen liegen. In Abb. 4a ist noch einmal gezeigt, was es mit den beiden geografischen Koordinaten eines Ortes, dem Breitengrad und dem Längengrad, auf sich hat. Liegen die beiden Schulen ungefähr auf dem gleichen Längenkreis (Abb. 4b), so ist das sehr gut. Wenn nicht, ist das auch nicht weiter schlimm, schließlich misst jede Schule die Schattenlänge zum "eigenen" Sonnenmittag. Wichtig ist nur, dass nicht die direkte Entfernung zwischen den beiden Schulen für die Berechnung genom­men wird, sondern der kürzeste Abstand zwischen den beiden Breitenkreisen (siehe Abb. 4c). Diese Entfernung lässt sich sehr leicht berechnen, wie wir gleich noch sehen werden.

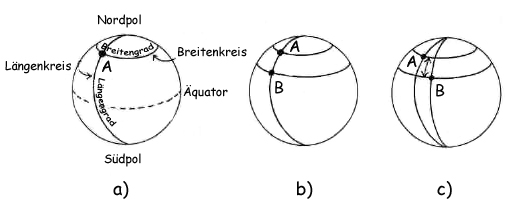
Abb. 4: Zur Bestimmung des Abstands zwischen den Breitenkreisen zweier Ort A und B

Man muss auch nicht bis zum Tag der Sommersonnenwende warten, um die Schattenlänge zu messen. Sie können dies an jedem beliebigen Tag des Jahres machen, wichtig ist nur, dass beide Schulen die Messung am gleichen Tag durchführen. Es wäre allerdings gut, wenn Sie die Messungen an mehreren Tagen wiederholen würden. Auch hier müssen Sie sich natürlich mit Ihrer Part­nerschule absprechen, an welchen Tagen dies geschehen soll. Jede Schule muss dann für sich den Zeitpunkt des örtlichen Sonnenmittags bestimmen (der von Ort zu Ort und an jedem Tag des Jahres verschieden ist). Den Zeitpunkt des Sonnenmittags an Ihrem Ort können Sie als Lehrerin vorab mit Hilfe der Tabelle zur Berechnung des Sonnenmittags schon mal heraussuchen, so dass Sie Ihre Schüler eine halbe Stunde um diesen Zeitpunkt herum nach dem kür­zesten Schatten suchen lassen können. Ein Kinderspiel! Vorausgesetzt die Sonne scheint.

Beispiel: eine Schule in Calais und eine Schule in Ajaccio

Die Koordinaten der beiden Städte sind: Calais: Breite 50°57'N, Länge 1°52'O; Ajaccio: Breite 41°55'N, Länge 8°43'O. Nehmen wir an, die beiden Schulen hätten Anfang Januar mit den konkreten Messungen der Schattenlängen be­gonnen. Sie haben an mehreren Tagen, jeweils zum Zeitpunkt des örtlichen Sonnenmittags, die Schattenlänge gemessen und ihre Werte mit der Partner­schule ausgetauscht. Sie stellen dann zum Beispiel fest, dass sie beide Mess­werte für den 23. Januar haben. Anhand dieser Messwerte können die Kinder dann mit Hilfe einer sehr einfachen geometrischen Zeichnung (Abb. 5) bis auf einen halben Grad genau den Winkel der Sonnenstrahlen mit der Senkrechten bestimmen (zum Zeitpunkt des örtlichen Sonnenmittags). Sie finden für Calais 68,5° (Winkel α₁) und für Ajaccio 59,5° (Winkel α₂) heraus.

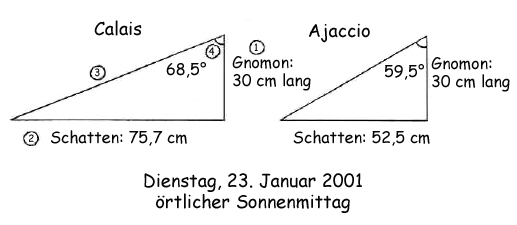
Abb. 5: Bestimmung der Winkel in Calais und Ajaccio

Und wie ermittelt man aus diesen beiden Werten nun den berühmten Winkel α (Abb. 6a)? Ganz einfach, indem man den Winkel α₂ vom Winkel α₁ abzieht, was 9° ergibt. Man kann diese Subtraktion auch zeichnerisch darstellen (Abb. 6b): Man zeichnet auf Pauspapier den Winkel α₂ und legt ihn so auf den Winkel α₁, dass die beiden der Sonne zugewandten Schenkel deckungsgleich sind. Der untere Schenkel des abgepausten Winkels ist dann parallel zur Senkrechten im Ort B, was dann wieder zur Zeichnung des Eratosthenes führt (siehe Abb. 3).

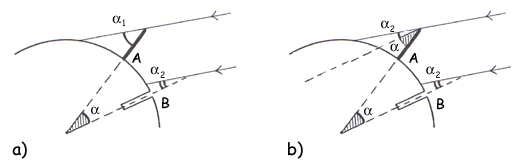
Abb. 6: Zur Bestimmung des Winkels α

Da die beiden Partnerschulen nicht auf dem gleichen Längenkreis liegen, muss jetzt die kürzeste Entfernung zwischen dem Breitenkreis von Calais und dem Breitenkreis von Ajaccio bestimmt werden, was ganz einfach ist: Auf eine Kar­te von Frankreich zeichnet man sorgfältig die beiden Breitenkreise ein und be­rechnet unter Berücksichtigung des Maßstabs der Karte die Entfernung zwi­schen den beiden Städten (Abb. 7). Für Calais un Ajaccio liegt der Wert bei ziemlich genau 1000 km.

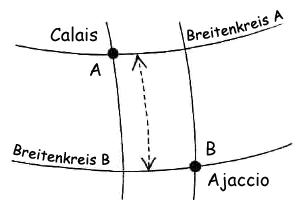
Abb. 7: Zur Bestimmung der Entfernung zwischen den Breitenkreisen von Calais und Ajaccio

Wir haben jetzt die beiden Größen, die notwendig sind, um den Erdumfang nach der Methode des Eratosthenes zu berechnen, nämlich den Winkel (9°) und die Entfernung zwischen den beiden Breitenkreisen (1000 km). Da das Verhältnis zwischen dem ermittelten Winkel und dem gesamten Kreis (9° zu 360°) 40 ist, bekommt man für den Erdumfang einen Wert von 40×1000 km, das heißt 40 000 km. Eine sehr einfache und praktische Methode zur Bestimmung des Erdumfangs, allerdings müssen die Messungen sehr genau durchgeführt werden, insbesondere wenn die geografischen Breiten der beiden Schulen näher beieinander liegen.

Anmerkung

Es ist interessant zu wissen, dass – wie aus Abb. 8 ersichtlich – die Differenz zwischen den beiden Breiten uns sofort den berühmten Winkel α liefert. Für die beiden Schulen aus unserem Beispiel kommt demnach 50°57' − 41°55' = 9°2' heraus. Die Schüler haben also sehr genau gemessen, denn der von ihnen ermittelte Winkel von 9° kommt diesem Wert sehr nahe.

Dieser direkte Weg zur Berechnung des Winkels sollte den Kindern natürlich zu­nächst auf keinen Fall mitgeteilt werden! Ihnen den Zusammenhang im Nach­hinein mitzuteilen, kann dagegen nützlich sein, um etwaige Fehler in ihren Messungen herauszufinden.

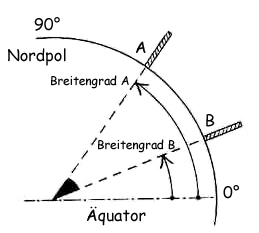
Abb. 8: Wie der Winkel α mit den Breitengraden zusammenhängt

Die verschiedenen Etappen des Projekts

Dieses Projekt ist für Schüler der Klassenstufen 4 bis 6 und für Oberstufen­schüler gedacht, doch können manche der in den ersten Etappen vorgeschla­genen Aktivitäten bereits in der Lernstufe 2 (1. bis 3. Klasse) durchgenommen werden. Den Grundsätzen von La main à la pâte entsprechend, sollte ganz besonders auf das eigenständige Nachdenken der Kinder geachtet werden. Sie sollten Hypothesen formulieren und sich die passenden Experimente ausden­ken, um diese Hypothesen zu überprüfen. Jeder Schüler sollte ein Experimen­tierheft führen, in das er mit Hilfe von Zeichnungen und kurzen Sätzen seine eigenen Nachforschungen festhält, außerdem die Ergebnisse der eigenen Grup­pe sowie die gemeinsam mit der ganzen Klasse erarbeiteten Zusammenfassun­gen. Dadurch können Sie überprüfen, ob die in der Klasse durchgeführten Akti­vitäten von den Kindern verstanden wurden, und Sie können die Entwicklung jedes Schülers verfolgen.

Wir schlagen Ihnen folgende Etappen vor:

1. Anmeldung und Durchführung der ersten Unterrichtseinheiten. Bei der An­meldung für das Eratosthenes-Projekt werden Sie automatisch in die Diskus­sionsliste für die am Projekt teilnehmenden Schulen mit aufgenommen. Sie können sich auf diese Weise mit den anderen beteiligten Lehrer austauschen. In der Liste sind auch Wissenschaftler und Pädagogen vertreten, die für die Beantwortung Ihrer Fragen verantwortlich sind.

2. Bei der Anmeldung erhalten Sie ein Passwort für den Zugang zum Online-Arbeitsbereich des Projektes. Dieser Arbeitsbereich erlaubt es jeder Klasse:

• ihre Messergebnisse auf der Webseite des Projektes zu veröffentlichen;
• die Koordinaten aller am Projekt beteiligten Klassen einzusehen;
• deren Messwerte abzurufen;
• den Standort der beteiligten Klassen auf einem Globus zu visualisieren;
• zur Erinnerung an das Projekt eine Postkarte zu schreiben, sie sich anzu­schauen oder zu verändern/ergänzen.

3. Während des gesamten Projekts können die Klassen ihre Messwerte in diesem Arbeitsbereich eintragen. Über die Diskussionsliste können simultane Messungen mit (einer) Partnerschule(n) geplant werden.

4. Am 21. Juni stellen die Klassen das historische Experiment nach, mit dem es Eratosthenes vor über zwei Jahrtausenden gelungen ist, den Umfang der Erde zu messen!

Letzte Aktualisierung: 24.1.2022