Winkelmessungen mit dem Eratosthenes-Gnomon

Publikation:	27.10.2007
Lernstufe:	3
Dauer:	Während mehrerer Wochen wird täglich – je nach Wetter – zum Sonnenmit­tag an einem sonnenbeschienenen Ort die Schattenlänge eines Gnomons gemessen (Dauer: 10 Minuten); im Klassenraum wird anschließend der Win­kel der Sonnenstrahlen grafisch bestimmt.
Material:	Für die gesamte Klasse: Eratosthenes-Gnomon Millimeterpapier gut gespitzte Bleistifte Lineale Winkelmesser Nähgarn
Herkunft:	La main à la pâte, Paris. Originalversion: www.fondation-lamap.org/eratos

Messungen der Schattenlänge

Jetzt geht's endlich richtig los mit dem eigentlichen Eratosthenes-Projekt!

Jeden Tag, wenn die Sonne mittags scheint und der Schatten des Eratosthe­nes-Gnomons sein "Treffen" mit der Mittagslinie einhalten kann, markiert ein Schüler mit dem Bleistift genau die Spitze des Schattens und misst sorgfältig dessen Länge.

Schematische Darstellung

Mit einem spitzen Bleistift überträgt er die Höhe des Gnomons und die Länge des Schattens (die auf den Millimeter genau zu messen sind – das ist sehr wichtig) in natürlichem Maßstab oder im Maßstab 1:2 auf Millimeterpapier und zeichnet dann die den Sonnenstrahl darstellende Gerade ein.

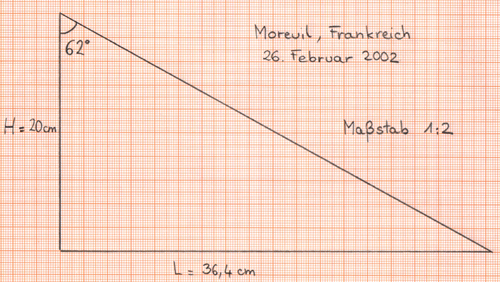
Abb. 4: Übertragung der Höhe des Gnomons und der Länge des Schattens auf Milli­meterpapier

Messung des Winkels

Dann bleibt nur noch mit einem Winkelmesser so genau wie möglich, d. h. auf einen oder einen halben Grad genau, den Winkel zu messen. Um eine noch höhere Genauigkeit zu erzielen, kann man wieder den Winkel auf Pauspapier übertragen und ihn auf die vergrößerte Fotokopie eines Winkelmessers legen (siehe Abb. 3).

Es empfiehlt sich, die Messung und die grafische Auswertung von drei Schülern parallel durchführen zu lassen, wobei alle natürlich denselben Schatten messen (deshalb ist das exakte Markieren der Schattenspitze so wichtig): Stimmen zwei oder drei Ergebnisse sehr eng miteinander überein, kann man diese als gültige Werte betrachten. Wenn die Werte zu sehr streuen, müssen die Zeich­nungen neu gemacht werden.

Eine fakultative Variante

Einige Schüler werden vielleicht versuchen wollen, den Winkel an Ort und Stelle zu messen, indem sie einen sehr feinen Faden (Nähgarn) von der Kante des Gnomons bis zur Spitze des Schattens spannen und den Winkelmesser an­legen. Sie werden feststellen, dass dies sehr schwierig ist. Insbesondere ist es nicht einfach, den Faden genau in der richtigen Position zu halten und den Winkelmesser in Bezug auf den Gnomon exakt auszurichten. Sie können jedoch ihre Ergebnisse mit den auf zeichnerischem Wege ermittelten Ergebnissen ver­gleichen und daraus ihre Schlüsse ziehen.

Man kann den Winkel auch auf sehr einfache und schnelle Weise an Ort und Stelle messen, und zwar durch direktes Anvisieren des kleinsten Schattens mit Hilfe eines so genannten Quadranten (dies hat uns letztes Jahr Gérard Corbet, Lehrer, vorgeschlagen): Siehe hierzu auch die fakultative Unterrichtseinheit "Messung des Winkels der Sonnenstrahlen mit einem Quadranten".

Bemerkungen

Im Laufe der Tage werden die Schüler feststellen, dass sich die Markierung der Schattenspitze entlang der Mittagslinie verschiebt: Ab dem 22. Dezember scheint sie zum Fuß des Gnomons zurückzukehren. Die Kinder werden daraus schließen, dass die Bahn der Sonne am 21. Dezember am tiefsten ist und an­schließend (bis zum 21. Juni) wieder steigt. Die Kinder sollten sich nun wieder die Tabelle mit den Messwerten für die Schattenlängen in Alexandria anschau­en und mit Ihrer Hilfe die Ähnlichkeit der Veränderungen der Schattenlängen im Jahresverlauf analysieren.

Und wenn eines Tages der Schatten des Gnomons die gleiche Länge hat wie der Gnomon selbst, werden Ihre Schüler sehen, dass der Winkel halb so groß ist wie der rechte Winkel, "wie wenn man ein Blatt über Eck faltet". An einem Ort mit einer geografischen Breite von 45° (in Bordeaux zum Beispiel, einer Stadt an der französischen Atlantikküste) tritt dieser Fall genau am 21. März, zur Tagundnachtgleiche ein. Zur Tagundnachtgleiche entspricht der Winkel der Sonnenstrahlen genau der geografischen Breite des Ortes. (Jede Schule, ganz gleich wo sie liegt, wird also an diesem Tag feststellen können, dass der ge­messenen Winkel so groß ist wie die geografische Breite des Ortes.)

Übermittlung der Messwerte an die Partnerschule(n)

Für jede Messung der Schattenlänge am Sonnenmittag werden der gemessene Winkel und das Datum (sowie die Uhrzeit, aber nur als Anhaltspunkt, sie wird für die späteren Berechnungen nicht gebraucht) sorgfältig auf der Zeichnung vermerkt.

Diese Informationen sollen auf der von La main à la pâte für das Projekt eingerichteten Internetplattform in eine Tabelle eingegeben werden, damit ihr eure Messwerte bekanntgeben und mit den über die ganze Erde verteilten Partnerschulen austauschen könnt. Geht dazu auf die Seite: https://eratosthenes.eu/wordpress/.

Denkt daran, dass ihr regelmäßig eure Messwerte veröffentlicht und die Ergeb­nisse der anderen Schulen verfolgt. Der Vergleich der Messwerte zwischen den verschiedenen Schulklassen ist Gegenstand der nächsten Projektphase, in der ihr u. a. mit den geografischen Koordinaten vertraut gemacht werdet. Bis bald im Internet!

© Sonnentaler/La main à la pâte | Impressum | Disclaimer | Datenschutz | RSS | E-Mail

© Sonnentaler / La main à la pâte  http://www.sonnentaler.net/